14

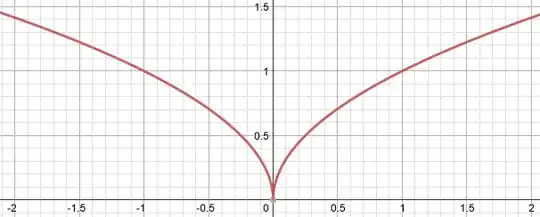
$f(x) = \sqrt{|x|}$ is a famous example of a function which is not Lipschitz continuous but is uniformly continuous. This link shows detailed explanation of it.

Here provides the figure of this function:

enter image description here

However, I am still confused about how to show $\sqrt{|x|}$ is not Lipschitz continuous?

  1. Consider $[-a,a]$, which is compact. $\frac{f(y)-f(x)}{y-x}$ should be bounded by $L$. This method is also used to prove $f(x)$ is a uniformly continuous.
  2. On $[a,\infty)$ and $(-\infty,-a]$, $f(x)$ has a bounded derivative.

So, based on 1 and 2, $f(x) = \sqrt{|x|}$ is Lipschitz continuous.

I have no idea how to prove it is not a Lipschitz continuous; clearly speaking I do not know how to distinguish the proof of Lipschitz continuity from uniformly continuity.

Community
  • 1
sleeve chen
  • 8,576
  • Suppose that the derivative IS bounded (by L). Then you can find $x_0$ such that $f'(x_0) \geq L$ – The Chaz 2.0 Jul 27 '15 at 17:12
  • Then I should ask the difference in the proof of uniformly continuous and Lipshitz continuous in this example. They look quite similar. – sleeve chen Jul 27 '15 at 17:14
  • Note that $f$ does not have a bounded derivative on $[-a,a]$ – Ben Grossmann Jul 27 '15 at 17:16
  • Maybe I get it. we prove Uniformly continuity by using limit but prove Lipshitz continuity by derivative. – sleeve chen Jul 27 '15 at 17:18
  • related – Ben Grossmann Jul 27 '15 at 17:19
  • Lipshitz condition $|f(x)-f(y)|\le L|x-y|$ means that $f(x)-f(y)$ becomes small as fast as $x-y$, i.e. at least linear decay. For uniform continuity it is enough that $f(x)-f(y)$ just becomes small as $x-y$ becomes small, but no demand on how fast. For example, the condition $|f(x)-f(y)|\le\sqrt{|x-y|}$ will give uniform continuity, but does not give Lipshitz, since $\sqrt{|x-y|}$ goes to zero too slow. – A.Γ. Jul 27 '15 at 17:36

3 Answers3

4

Consider only the interval $[0,a]$ for some $a>0$ and suppose that $f(x)=\sqrt{|x|}$ is Lipschits: $|f(y)-f(x)|\leq L|y-x|$. Then for $x=0$ and $y<a$ we should have:

$|\sqrt{y}|\leq L|y|\Leftrightarrow \sqrt y\leq Ly\Rightarrow \frac{\sqrt y}{y}\leq L$ for each $y>0$. But this is impossible since for $y\rightarrow 0^+$, the LHS tends to $+\infty$.

Svetoslav
  • 5,325
3

The derivative of $\sqrt{|x|}$ is $\frac{\mathbb{sgn}(x)}{2\sqrt{|x|}}$. Let $x_0 = \frac{1}{4L^2}$. The derivative at $x_0$ is $L$, so, the derivative is unbounded.

lisyarus
  • 17,012
  • The derivative at $x_{0}$ is $L$ then why the derivative is unbounded, I only see it becomes unbounded at $x=0$? – BAYMAX Sep 15 '18 at 10:09
  • 1
    @BAYMAX Here, we talk about the derivative being unbounded on a whole set $[a, +\infty)$ (where $a>0$), not at one exact point. Since for any $L > 0$, there exists a point $x_0 \in [a, +\infty)$ where the derivative is $L$, we conclude that the derivative is unbounded globally. – lisyarus Sep 15 '18 at 12:04
  • @BAYMAX Oh, I apologize. I meant $(0, +\infty)$ instead of $[a, +\infty)$. – lisyarus Sep 15 '18 at 12:49
1

The function you seem to consider in 1. is not even defined everywhere. What should it be for $x=y$? Thus this argument does not work.

The "problem" occurs around $0$. Assume the function is Lipschitz with constant $C$. Then $|f(x)-f(0)| \le C |x-0|$ for all $x$. So $f(x)/|x| = \sqrt{|x|}/|x| \le C$ for all $x$ which is not true.

quid
  • 42,835
  • To the first part, if your claim is true, then we cannot find a function which is differentiable because we could always make $x = y$ – sleeve chen Jul 27 '15 at 17:28
  • It seems that in 1. you try to use the result that a continouus function on a compact set is bounded. If you want to use this result you need a continous function on a compact set. What is you function and what is your set? (Or what are you trying to say in 1?) – quid Jul 27 '15 at 17:34
  • $[-a,a]$ is a set in $\mathbb{R}$, for example $[-5,5]$. I make an error in 1. i.e. the derivative is not bounded. – sleeve chen Jul 27 '15 at 17:38