Hypercube and Hyperspheres

Question

Let $n,k\in\mathbb{N}$. In this problem, the geometry of $\mathbb{R}^n$ is the usual Euclidean geometry.

The lattice hypercube $ Q(n,k)$ is defined to be the set $ \{1,2,...,k\}^n \subseteq\mathbb{R}^n$. If we want to cover this hypercube with the $m$ distinct $(n-1)$-dimensional hyperspheres $S_1$, $S_2$, $\ldots$, $S_m$. By "covering $Q(n,k)$," I mean that $Q(n,k)\subseteq \bigcup\limits_{j=1}^m\,S_j$. What is the least possible value of $ m$?

Using a simple Combinatorial Nullstellensatz argument, we can show that if $ \mu(n,k)$ is the minimum possible $ m$, then $$ 1 + n\left\lfloor\dfrac{k - 1}{2}\right\rfloor \leq \mu(n,k) \leq 1 + n\left\lfloor\left(\dfrac{k - 1}{2}\right)^2\right\rfloor \,. $$ However, the lower bound is not sharp for large $ k$. All I know is that the lower bound is exact for $ k = 1$, $ 2$, $ 3$, and $ 4$, as well as when $ n = 1$, and for a special case with $ n = 2$ and $ k = 5$ (as shown in the attached figure below). While my bounds give $5\leq \mu(2,6) \leq 13$, I believe that $\mu(2,6)=6$. Can you verify this?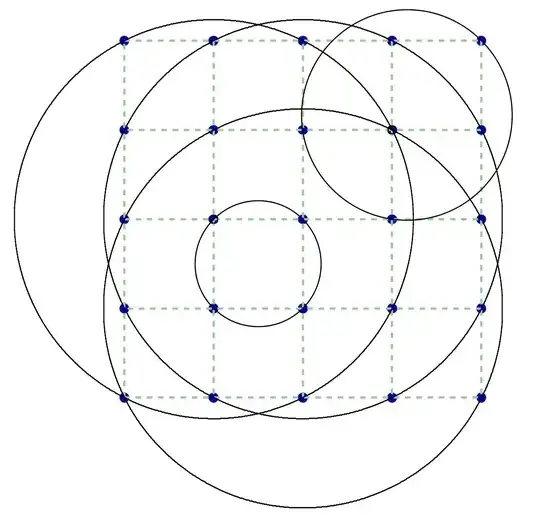

Can anyone help improve these bounds? Note that the bounds also work if the $S_j$'s can be $(n-1)$-dimensional hyperellipsoids, but what will be the value of the smallest $m$ in this case (which, to avoid confusion, we shall use $\nu(n,k)$ for this smallest $m$)? In other words, we also have $$ 1 + n\left\lfloor\dfrac{k - 1}{2}\right\rfloor \leq \nu(n,k) \leq 1 + n\left\lfloor\left(\dfrac{k - 1}{2}\right)^2\right\rfloor \,. $$
For example, $\nu(1,k)=\left\lceil\dfrac{k+1}{2}\right\rceil=\mu(1,k)$ for all $k\in\mathbb{N}$ and $\nu(2,k)=1+2\left\lfloor\dfrac{k-1}{2}\right\rfloor$ for $k=1,2,3,4,5$. Observe that the lower bound for $\nu(2,6)$ is also sharp (i.e., $\nu(2,6)=5$).

What happens if the $S_j$'s can be any nondegenerate $(n-1)$-dimensional hyperconic sections (where my Combinatorial Nullstellensatz argument no longer works, so the lower bound I have obtained no longer holds)? In this most general form, we shall use the notation $\rho(n,k)$ for the smallest $m$. The only known bound for $\rho(n,k)$ is $$ \rho(n,k) \leq 1 + n\left\lfloor\left(\dfrac{k - 1}{2}\right)^2\right\rfloor \,. $$ For example, $\rho(1,k)=\left\lceil\dfrac{k+1}{2}\right\rceil=\mu(1,k)$ for all $k\in\mathbb{N}$. However, $\mu$, $\nu$, and $\rho$ do not always coincide. Known values are $\rho(2,1)=1=\rho(2,2)$ and $\rho(2,3)=2<\mu(2,3)$, while we have $\rho(2,4)\leq 3=\mu(2,4)$, $\rho(2,5)\leq 4 <\mu(2,5)$, and $\rho(2,6)\leq 5\leq\mu(2,6)$.

Answer 1

Here's a result for $n=2$.

As discussed at Bounds for the size of a circle with a fixed number of integer points, a circle of radius $R$ centred at the origin passes through at most $4(2\log_5R+1)$ integer lattice points.

Our circles need not be centred at the origin, but we can get an upper bound for the denominator of the rational coordinates of their centres. Assume that at least three integer lattice points $(x_i,y_i)$ lie on a circle centred at $(X,Y)$. Then subtracting the three circle equations yields

$$ x_1^2-x_2^2+y_1^2-y_2^2=2X(x_1-x_2)+2Y(y_1-y_2)\;,\\ x_1^2-x_3^2+y_1^2-y_3^2=2X(x_1-x_3)+2Y(y_1-y_3)\;. $$

This is a linear system of equations for $X$, $Y$ with integer coefficients, and the denominator of the solution is at most $2$ times the determinant

$$ \left|\begin{matrix}x_1-x_2&y_1-y_2\\x_1-x_3&y_1-y_3\end{matrix}\right|\;. $$

(Not $4$ times because one factor of $2$ is also in the determinants in the numerator.) This is the area of a parallelogram spanned by the three points, which can be at most $(k-1)^2\lt k^2$, so the denominator is at most $2k^2$. We can subdivide the grid by the denominator; all lattice points will still be lattice points, and the radius of a circle of radius $r$ in terms of the new grid constant will be at most $R=2k^2r$. Thus a circle of radius $r$ can pass through at most $4(2\log_5(2k^2r)+1)$ lattice points.

Now we need to bound the radius $r$. Again assume that at least three lattice points $(x_i,y_i)$ lie on the circle. Then the area of a parallelogram they span is a positive integer, and hence at least $1$. Since the distance between two of them is at most $\sqrt2(k-1)$, the altitude of the third above the line connecting them must be at least $1/(\sqrt2(k-1))$. For at least one of the points, this altitude intersects the opposite side. Then for given altitude, the radius of the circle is maximal if the point is symmetrically positioned between the other two points. This maximal radius is the radius of the circle that passes through $(\pm (k-1)\,/\sqrt2,0)$ and $(0,1/(\sqrt2(k-1)))$, which is

$$ r_\text{max}=\sqrt{\frac{(k-1)^2}2+\frac{\left((k-1)^4-1\right)^2}{8(k-1)^2}}\le2^{-3/2}k^3\;. $$

Plugging this into the bound derived above yields

$$ \mu(2,k)\ge\frac{k^2}{4\left(2\log_5(2^{-1/2}k^5)+1\right)}\sim\frac{\log5}{40}\frac{k^2}{\log k}\approx\frac1{25}\frac{k^2}{\log k}\;. $$

This improves on your linear bound for $k\ge122$.

This could probably be improved by a more careful analysis, since circles of radius $k^3$ are very close to a line passing through the grid; at the very least the factor $4$ can asymptotically be replaced by $2$ since at most $2$ quadrants of such a large circle can intersect the lattice.

---

I removed some optimistic remarks about generalizing this for higher $n$. While the argument for the denominator generalizes and yields $R\le2k^nr$, and I believe the argument for the maximal radius should also generalize and again yield a bound of the order of $k^3$, what's missing to turn this into improved bounds for the present problem is a logarithmic bound on the number of lattice points on a hypersphere. In fact the MathWorld article on the sum-of-squares function gives identities that imply that such a bound doesn't hold for many $n$.

Here, in case someone can make use of them, are some results I found in the literature. This paper (for $n=3$) and this paper (for $n\ge4$) give bounds for the difference $\Delta_n(R)$ between the number of lattice points inside an $(n-1)$-sphere of radius $R$ and its volume:

$$ \begin{align} \Delta_n(R)\in O\left(R^\theta\right)\quad\text{with}\quad\theta= \begin{cases} \frac{21}{16}+\epsilon&n=3\\ 2+\epsilon&n=4\\ n-2&n\ge5 \end{cases} \end{align} $$

Since the number of lattice points in the sphere jumps by the number of lattice points on the sphere, the latter must satisfy the same bounds.