Assume the following is in in $\mathbb{R}^n$
1. If $d_i,d_j$ are orthogonal with $i \neq j$, it means $d_i^Td_j=0$.
2. If $d_i,d_j$ are $A$-orthogonal with $i \neq j$, it means $d_i^TAd_j=0$.
In many lecture, it can be viewed as the following:
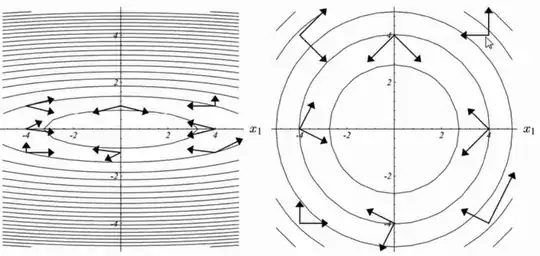
The left is $A$-orthogonal, the right is orthogonal. Why?
It seems this is related to the rotation and decomposition of a matrix. However I am weak in this part. Could anyone give me a clear explanation of it?
The circles in the right image can be interpreted as level curves of $x^TAx$. In particular, if $A=I$, then the level curves in $\mathbb R^2$ are circles. Also, in this case, orthogonal vectors have the usual geometric interpretation of being "perpendicular". That's why the vectors drawn in the right image are "perpendicular".
Analogously, the ellipses in the left image are level curves of $x^TAx$. Let's say $A=\begin{bmatrix} 1& 0\\0& 3\end{bmatrix}$ and $x^TAx=3$. You get the equation of an ellipse: $x_1^2+3x_2^2=3$. Two vectors that are $A$-orthogonal are $[1\ 1]^T$ and $[-3\ 1]$. Plot them and they have a large angle between them.
