2

My book (Introduction to Ring Theory, Paul Cohn) states this as a theorem and gives a proof. The book usually skips over trivial/easy proofs, so I don't really understand why this is in here.

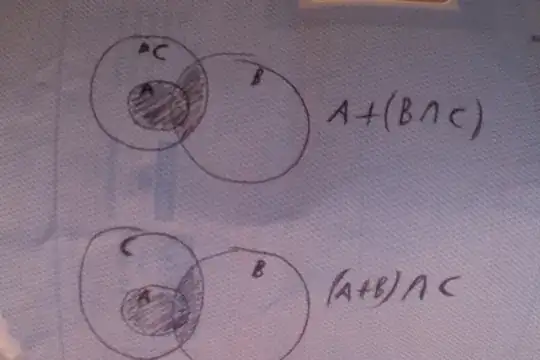
Isn't the statement absolutely obvious for sets $A,B,C$ with $A\subseteq C$? You just need to draw a diagram and it becomes immediately obvious! enter image description here

Is there a reason why it would not be obvious in modules?

man_in_green_shirt
  • 2,676

2 Answers2

4

I'm not sure if the statement is obvious to you but in general $+$ and $\cap$ don't distribute over each other. I wouldn't expect them to either since $\cap$ is a set theoretic operation and $+$ is only defined for modules/ideals/abelian groups. However, when $A\subset C$ they do distribute over one another.

But the proof shouldn't go something like this:

$$A+(B\cap C)=(A+B)\cap (A+C)=(A+B)\cap C $$ where the last equality comes from $A\subset C$ because here we assumed they distribute in the first place which is false in general. So any proof of this fact can't use the above method (or the other direction).

An explicit example that these operations don't distribute is by taking the submodules of the $\mathbb{Z}[X]$-module $\mathbb{Z}[X]$ where we can now just look at ideals

$A=(2)$, $B=(x-1)$, and $C=(x+1)$ then $$A+(B\cap C)=(2)+(x^2-1)=(2,x^2-1)$$ and $$A+ B \cap A+ C=(2,x-1)\cap(2,x+1)=(2,x+1)$$

since $(2,x-1)=(2,x+1)$.

Eoin
  • 6,049
  • I've added a picture of what I meant. If you just draw them as sets and then colour in the relevant parts, you can see that they're the same. This is what I meant by 'obvious' – man_in_green_shirt Jul 14 '15 at 16:59
  • 1
    @man_in_green_shirt Although instructive, the $+$ operation in your picture is really $\cup$ in which case $\cap,\cup$ do distribute over each other. Essentially you are assuming they distribute over each other (as I say above) which is not true. – Eoin Jul 14 '15 at 17:07
  • 1
    Oh ok, that's what my misunderstanding was, I was reading '+' as 'union', when $A+B$ should actually be the set of all $a+b$ where $a\in A,b\in B$ – man_in_green_shirt Jul 14 '15 at 17:10
  • Sorry, one more question: why is $B\cap C=6 \mathbb{Z}$? Aren't we looking for the integers which are multiples of both 12 and 30? 6 isn't a multiple of either. Why wouldn't the answer be $60\mathbb{Z}$? – man_in_green_shirt Jul 14 '15 at 17:20
  • 1
    @man_in_green_shirt You're right, let me fix the example. – Eoin Jul 14 '15 at 17:28
  • @man_in_green_shirt Fixed. And completely new! – Eoin Jul 14 '15 at 17:44
  • Nice example! Although shouldn't there be a $+$ instead of a $\cap$ in the middle part of the first line? – man_in_green_shirt Jul 14 '15 at 17:46
3

Judging from your diagram, it looks like (?) you are interpreting $+$ as set union. Certainly, if you are working with sets using union and intersection, your picture is accurate.

But using using the $+$ to join submodules of a module does not behave the same way. If $A$ and $B$ are submodules of a module, $A+B$ contains many more elements than just $A\cup B$ in general.

To summarize the situation, the property proved is that the lattice of submodules of a module (join $+$ and meet $\cap$) is a modular lattice. The lattice of subsets of a set, on the other hand (join $\cup$, meet $\cap$), is also modular, but even more strongly it is a distributive lattice. In general, the lattice of submodules of a module does not have to be distributive.

For more about modularity, let me refer you to a question we had some time ago on the topic: Why are modular lattices important?

Community
  • 1
rschwieb
  • 160,592
  • 1
    Yes, that was how I was interpreting the '+', when I should have interpreted it as $A+B$ being the set of all $a+b$ where $a\in A, b\in B$. thanks! – man_in_green_shirt Jul 14 '15 at 17:12