21

The Laplacian of the graph has all the eigenvalues real and non-negative, the smallest being 0. I have a graph where the second smallest eigenvalue (the so called algebraic connectivity) is equal to $1$. In fact, the multiplicity of this eigenvalue is quite high: in other words, many eigenvalues of the Laplacian are equal to $1$.

What can we say about the graph when many eigenvalues of the Laplacian are equal to 1? For example, eigenvalue $0$ implies that the row sum is $0$. What about eigenvalue $1$ with high multiplicity?

In my case, the Laplacian is defined as $L = D - A$, where $D$ is the degree matrix (diagonal matrix with degree values on the diagonal) and $A$ is the adjacency matrix of the graph.

Peaceful
  • 581
  • 1
    I don't think this enough for a full answer so I'll just comment: I think a useful observation may not be that your second eigenvalue is $1$ with great multiplicity, but that your third, fourth, fifth, etc. are all $1$. The tightness in between these successive eigenvalues may produce some interesting results. – muaddib Jun 25 '15 at 12:36
  • 2
    For example, in this paper http://www.fmf.uni-lj.si/~mohar/Papers/Spec.pdf referenced by the algebraic connectivity wiki page, When you add an edge to a graph, the spectrum of the graph with the additional edge interlaces with the spectrum of your original graph. In your case, that means the spectrum of the supergraph will have one less $1$ eigenvalue. – muaddib Jun 25 '15 at 12:36
  • Thanks for this. I will look at it. Do you know any literature about the multiplicity of algebraic connectivity? – Peaceful Jun 25 '15 at 15:34

2 Answers2

14

I can make two sort of hand-wavy observations. From basic linear algebra properties we know that given a matrix $ \mathbf{L} $ \begin{equation} \sum_{i}d_{i}= \sum_{i}\lambda_{i} \end{equation}

where $ \lambda $ are the eigenvalues, and $ d $ are the the diagonal elements of your matrix $ \mathbf{L} $.

The elements on the diagonal of the Laplacian correspond to the degrees of the vertices. Assuming no isolated vertices and that the graph is simple (i.e weights are either $0$ or $1$), $ d_{i} \geq 1 $.

If most of your eigenvalues are equal to $1$, then their sum is also likely a small number. That means that the sum of degrees is also a small number, which means that your graph is probably sparsely connected.

The next observation has to do with star graphs. In general, complete bipartite graphs with $n$ and $m$ vertices on each group respectively, have Laplacian eigenvalues:

  • $n$ with multiplicity $m-1$
  • $m$ with multiplicity $n-1$
  • $0$ with multiplicity $1$
  • $m+n$ with multiplicity 1

Consider the star graph below which is a complete bipartite graph with $n=1$ and $m=8$

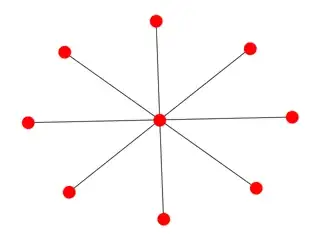
enter image description here

Its eigenvalues are $1$ with multiplicity $7$, $0$ with multiplicity $1$ and $9$ with multiplicity $1$.

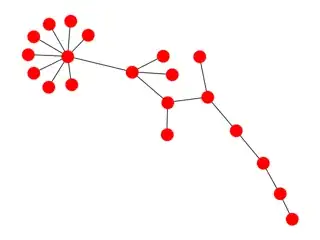
So, if your graph contains starlike subgraphs, then your Laplacian is going to have a bunch of $1$-eigenvalues. I include two examples below (the isolated component belongs to the graph on the right).

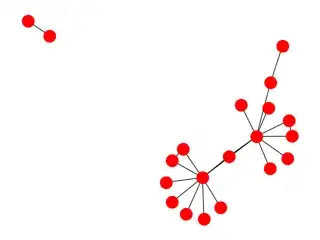
enter image description here. enter image description here

Both of these graphs have eigenvalue $1$ with multiplicity $9$.

Aspect Stalence
  • 437
2

I would add to @Aspect's excellent answer an eigenvector and graph symmetry point of view.

For the combinatorial Laplacian, $L=D-A$, the eigenvectors to eigenvalue $1$ of the star graph are $(0,1,-1,...,0)$, $(0,1,0,-1,...,0)$ $...$ $(0,1,0...,0,-1)$, where the first coordinate corresponds to the central vertex.

This reflects the symmetry of the graph in exchanging these leaf or pendant vertices attached to the same central vertex.

This symmetry remains in place for the star's leaves even if one of these 'legs' or 'rays' are connecting 'beyond the star' because the eigenvector only 'sees' $2$ leaves.

Michael T
  • 1,742