12

I'm reading Hartshorne AG V.3 on monoidal transformations and embedded resolutions. I understand one sort of intuition behind blowing up a point on a surface (or more generally a subvariety of a nonsingular variety), which is that you replace the point with the projective space of normal directions to the point. With this in mind, it is clear that two curves meeting transversally at a point in a surface $X$ separate in the blowup of $X$ along the point of intersection.

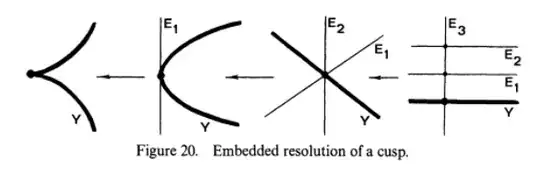
A case that I do not have a good feel for is the cusp ($y^2=x^3$ in the plane). Hartshorne V.3 Figure 20

It's not hard to write down equations in this case. However, what I would like to know is if there is any good geometric rationale that one can "tell just by looking" that blowing up the cusp gives a strict transform which is tangent to the exceptional divisor at a point? Considering only the first monoidal transformation above, why might it be obvious that the strict transform does not cross the exceptional divisor transversely?

Community
  • 1
Cass
  • 3,105

2 Answers2

7

The blowup replaces the origin by copy of $\mathbb P^1$, which you can think of as a little circle at the origin. That is, the blowup is the same as $\mathbb A^2$ away from the origin, but has a whole $\mathbb P^1$'s worth of extra points lyng above it, which you can think of as recording the different directions at the origin. When you take the proper transform of a curve, the portion of it that went through the origin is replaced by the direction it was going as it passed through.

With the cusp for $y^2 - x^3$, the curve goes into the origin horizontally and comes back out horizontally-- and it does it at such a rate to "just touch" the $\mathbb P^1$ at the point corresponding to the horizontal direction.

(Notice that $y^2 - x^5$ looks a lot like $y^2 - x^3$, but when you blow up it's still singular, so there is a bit of a limitation to this sort of visualization. I think it works best for curves like $y^2 - x^3 - x^2$ that cross through transversely a couple times. There the fibre of the proper transform above the origin will consist of the two different directions that the curve was going when it passed through).

Phil Tosteson
  • 1,901
  • 1
    When you say "at such a rate," are you not really conceding that you can't tell from the picture? I think your example of y^2=x^5 is good in showing that you can't decide the picture of the strict transform simply by looking at the graph of the original curve. However, in both cusp examples, it is not the case that the strict transform crosses the exceptional divisor transversely. So it seems there may still be hope for a pictorial argument which says "cusp" implies "nontransversal meeting with E". – Cass Jun 16 '15 at 04:13
  • I'm not conceding anything-- just trying to give context. There is a difference between the two graphs: the $y^2- x^5$ goes into the origin more sharply. My picture is that if you leave the origin going the same direction as you entered, then you cannot have passed through the exceptional divisor. The proof is in the algebra. – Phil Tosteson Jun 16 '15 at 04:27
0

Thought about it some more and you can see it from the following picture. Imagine the family of nodal curves with fixed node at the origin degenerating to a cusp: in this case $y^2=x^2(x+t)$. At the origin for $t\neq 0$, there are two directions on the curve normal to the point, and if $t$ is very small then both are almost horizontal. So each nodal curve gives two points on the exceptional divisor when blowing up the plane at the origin, and these two points come together at $t=0$ to a point of multiplicity $2$, which is the second picture in the figure above.

Cass
  • 3,105