1

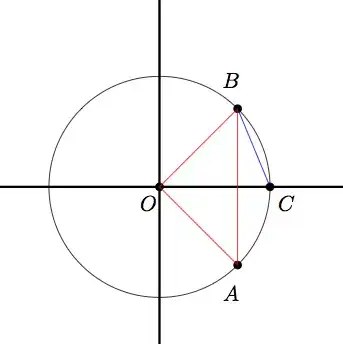
So I have to prove that $$ t= \sqrt{2-\sqrt{4-s^2}} $$

If I have a n-gon with side length s inscribed in a unit circle then bisect it to create a 2n-gon with side length t, there should be some relationship, right? I'm not even sure how to relate them? Area? Sides? Angles? Pythagorean theorem?

I even tried drawing it with compass. No luck. Help?

Stephanie Hernandez
  • 477
  • 1
  • 3
  • 11

1 Answers1

0

Hint:

If the angle at the center for the $n-$gon is $2\alpha$ we have:

$$ s=2\sin \alpha \qquad t=\sqrt{(1-\cos \alpha)^2+\sin ^2\alpha} $$

Calculating $t$ and substituting $s$ you have the result in OP.

$\angle BOA=2\alpha \Rightarrow \angle BOC = \alpha$

$BA=s \qquad BC=t$

enter image description here

Emilio Novati
  • 64,377