4

sorry for lame question, but I just have no maturity in this direction.

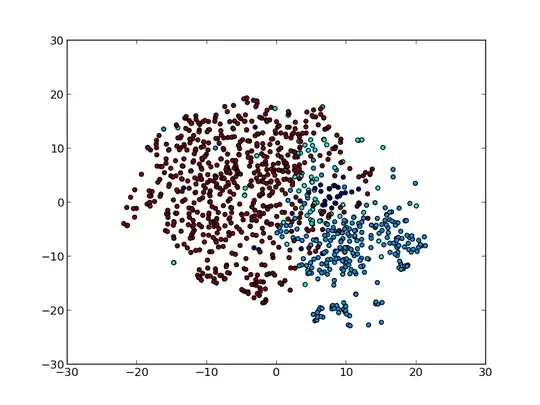
Let's say I have very large set ( millions ) of high-dimensional vectors ( typical dimensionality is 64). These vectors typically come from embedding of social network into a vector space, but this is not so important. Here is what we see using tSNE, for example: embedding example

We know, that sometimes some subsets of these points could form almost regular lattices like that: 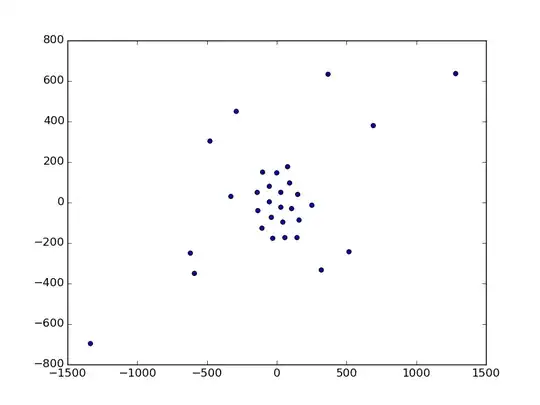regular lattice example I need either: 1. To prove, that no such structures exist 2. Or find all these structures ( if any )

But the hard part of a problem is that these regular structures could be different, and no one can say -- what type of lattice could approximate these better than another?

It seems, that I have to find some clusters in my vector space, which are not just "dense", but also have some unknown form of regularity. And typical algorithms like DBSCAN or MeanShift will not help me much.

So, could you please give me a couple of hints : what articles to read on this subject ( at least to have more clear problem statement )?

Vast Academician
  • 163
  • 1
    (+1) I don't think this is a lame question :) - and I definitely don't know how to do it. – Peter Woolfitt May 07 '15 at 19:24
  • To start with, I would read about Bravias lattices in 2D and 3D. In 3D, crystallography does stuff like this, look up 'crystal symmetry groups'. In 64D... It's very hard:) – Valentin May 07 '15 at 19:41
  • Maybe look for peaks in the Fourier transform? I don't know if that's practical in high dimensions. –  May 07 '15 at 19:43
  • Thank you, colleagues ( and @Rahul especially )! I was thinking about k-space approximation, but just wasn't certain about the simplicity of this approach. Basically, I'm trying to solve this task in two steps: 1) Apply conventional density clustering to isolate areas with apparently high density ( i.e. such lattices are likely to be there ), 2) Build BSP tree in each high-density region, and then count the sample entropy of each leaf. If the entropy is at maximum, then it's likely, that points are regularly spaced. – Vast Academician May 07 '15 at 22:04

1 Answers1

0

http://ipht.cea.fr/Docspht/articles/t10/051/public/merw-review.pdf -- just FYI. If someone still interested, I decided to use maximum entropy random walk ( MERW ) in my vector space to separate regions with high density and regular structural properties, because it seems that MERW have very good localization properties in face of defects.

The one differentiation point between my approach and the cited article is that I think of empty space as of "imperfection", and this makes MERW concentrate much in symmetric areas ( because these have least potential )

Also another article, supporting my hypothesis : http://arxiv.org/abs/1301.0725 It seems, that this index should have similar properties. But anyway, I wish to thank everyone for valuable hints!

Vast Academician
  • 163