9

The question is to find $x$ in:

\begin{equation*} x^2=e^x \end{equation*}

I know Newton's method and hence could find the approx as $x\approx -0.7034674225$ from

\begin{equation*} x_{n+1} = x_n - \dfrac{x_n^2-e^{x_n}}{2x_n-e^{x_n}} \end{equation*}

According to WolframAlpha:

x^2=e^x

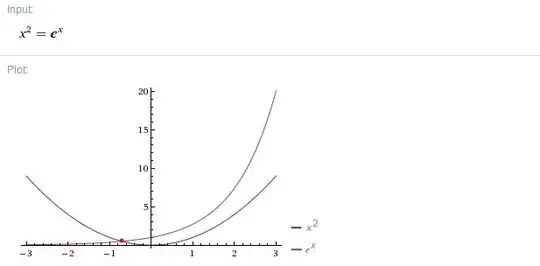
They also say that $x=-2W(\dfrac{1}{2})$ which shows that it can be solved using some Lambert-W function...Can anyone tell me how to do this?

Thanks a lot!

P.S. - I studied a li'l bit of Lambert-W ... So i guess a detailed explanation would not be needed ... just the initial steps!

Claude Leibovici
  • 289,558
NeilRoy
  • 2,251

4 Answers4

11

$$ x^2=e^x\implies x/2=\pm\tfrac12e^{x/2}\implies-x/2\,e^{-x/2}=\pm\tfrac12 $$ Therefore, $$ x=-2\mathrm{W}\!\left(\pm\tfrac12\right) $$ Since $\mathrm{W}(x)$ is real only for $x\ge-\frac1e$, we only have one real solution: $$ x=-2\mathrm{W}\!\left(\tfrac12\right)=-0.70346742249839165205 $$

robjohn
  • 353,833
  • How did you know that $-2W(\dfrac{1}{2})$ approximates to $-0.703467...$? – NeilRoy May 07 '15 at 14:45
  • Mathematica has the LambertW function. I have also detailed an algorithm to compute $\mathrm{W}(x)$ in this answer. Five iterations of that algorithm give over $12$ places of accuracy. – robjohn May 07 '15 at 14:51
9

The Lambert W function is the inverse of $xe^x$. We want to find the inverse of $e^x x^{-2}$, dividing by $x^2$.

Now: \begin{align} y &= x^{-2} e^x \\ y^{-0.5} &= x e^{-0.5x} &&\vee y^{-0.5} = -x e^{-0.5x} \\ -0.5y^{-0.5} &= -0.5x e^{-0.5x} &&\vee 0.5y^{-0.5} = -0.5x e^{-0.5x} \\ W(-0.5y^{-0.5}) &= -0.5x &&\vee W(0.5y^{-0.5}) = -0.5x \\ x &= -2W(-0.5y^{-0.5}) &&\vee x = -2W(0.5y^{-0.5}) \\ \\ \end{align}

Now we have y=1, so $x=-2W(-0.5)$ or $x=-2W(0.5)$. The first one is complex, so only the second one remains as real solution.

wythagoras
  • 25,726
8

Write the equation as $x^2e^{-x} = 1$. Then $x^2e^{-x} = 4\left(\left(-\frac{x}{2}\right)e^{-\frac{x}{2}}\right)^2$.

Lukas Betz
  • 4,606
-1

You can write $\mathrm{f(x)=e^{-x}.x^2}$ Now differentiate this function w.r.t x. $$\mathrm{f`(x)=e^{-x}(2x-x^2)}$$. Now set $$\mathrm{f'(x)=0}$$. It yields the solutions $$\mathrm{x=0 and x=2}$$. The values of f(x) at these x values are 0 and $\mathrm{4/e^2}$ respectively. Obviously $\mathrm{4/e^2}$ is less than 1. Now plot the graph of this function. Find the number of intersection points of this function and $\mathrm{y=1}$.

satyass16539
  • 1