Random Walk Without Repetitions

Question

Suppose that we simulated a random walk on $\mathbb Z$ starting at $0$. At each step, we transition from position $x$ to position $x-3,\,x-2,\,x-1,\,x+1,\,x+2,$ or $x+3$ with equal probability. If we ever move to a position we have been at before, we stop. What is the probability that we will eventually reach (and stop at) $0$ again?

This is to say, we consider that walks like $0,2,4,3,2$ end at $2$ because they repeated and walks like $0,2,4,3,1,0$ reach $0$ again - and are interested in the probability of the latter case.

I'm not sure what methods I can use to dispatch such a problem; if the step size were $1$ rather than $2$, the answer is obviously $\frac{1}2$, as we would need to immediately undo our first step, otherwise we'd never return. If the step size is $1$ or $2$, then we can solve the problem by noting that we can never leap over any pair of positions $(x,x+1)$ - which allows us to classify and count every possible walk (e.g. walks of the form $0,1,3,5,\ldots,2n+1,2n,2n-2,\ldots,0$ form one class). The probability of returning to $0$ is $\frac{7}{18}$ in this case. However, no such approach extends to the case above. By simulating all random walks of length $8$ or less, I have proven that the probability $p$ satisfies $.32<p<.39$. Running many random trials suggests that $p$ is very close to the lower bound.

Answer 1

First let's consider a closely related enumeration problem.

Define the range of a cycle $\{x_0, x_1, x_2, \ldots, x_{k-1}, x_k=x_0\}$ to be $\max_i \left|x_{i+1}-x_i\right|$. How many cycles on $\mathbb{Z}$ are there with $k$ edges and range $\le r$? (Two cycles are equivalent if they differ by a translation or a rotation.)

If $N_k^{(r)}$ is the number of cycles with $k$ edges and range no greater than $r$, then the probability of returning safely to $0$ by making random jumps of length $\le r$ is given by $$ P^{(r)}=\sum_{k=2}^{\infty}\frac{kN_{k}^{(r)}}{(2r)^{k}}. $$ The factor of $k$ is needed because the starting point ($0$) can be identified with any of the nodes in a given cycle; and the factor of $(2r)^{-k}$ is the probability of taking any specific sequence of $k$ jumps. For $r=1$, there is only one legal cycle (a jump to the right and then a jump to the left), and it has two edges, so $$ P^{(1)}=\frac{2 N_2^{(1)}}{(2r)^{2}}=\frac{2\cdot 1}{(2\cdot 1)^2}=\frac{1}{2}. $$ For $r=2$, there are two cycles for each $k\ge 2$ (depending on whether the first rightward jump is $+1$ or $+2$), so $$ P^{(2)}=\sum_{k=2}^{\infty}\frac{kN_k^{(2)}}{(2r)^k}=2 \sum_{k=2}^{\infty}k 4^{-k}=-2x\frac{d}{dx}\sum_{k=2}^{\infty}x^{-k}\bigg\vert_{x=4}=-2x\frac{d}{dx}\left(\frac{1}{x(x-1)}\right)\bigg\vert_{x=4}=\frac{2(2x-1)}{x(x-1)^2}\bigg\vert_{x=4}=\frac{2\cdot 7}{4\cdot 9}=\frac{7}{18}. $$ This recovers the two known results. For $r\ge 3$, the desired enumeration can be done using a transfer matrix method. I'll make this answer "community wiki" in case someone (maybe me) has the time and energy to fill in the details for $r=3$.

---

The gist of the transfer matrix approach is that we can list the "states" that a particular node in the cycle can have, figure out which state-to-state transitions are allowed moving from left to right on the number line, and express the number of ways to get from the left end of a cycle to the right end (i.e., the number of different cycles) in terms of a product of many identical local matrices. In this case the "state" consists of the set of jumps to, from, and over the node, along with the range remaining to each jump. Because we're counting cycles, each node will have exactly one incoming edge and one outgoing edge. The states for $r=2$ are simple:

A blue (red) line represents a jump to the right (left), and the number next to a line indicates its remaining range. A legal transition consists of these steps:

• Decrement all numbers on the right edge by the same value (at least $1$, but no more than the smallest number on the tile).
• Select a new tile with the same number of blue and red lines on its left edge as the current tile has on its right edge.
• Place the new tile to the right of the current tile and connect lines of the same color. Make sure that all lines that pass through the new tile maintain their (decremented) values.

Legal transitions for $r=2$ are: $A$ to $(B,C,D)$ (and $A$ to $D$ can happen two ways), $B$ to $(C,D)$, and $C$ to $(B,D)$. The corresponding transfer matrix is $$ \left(\begin{matrix}0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 2 & 1 & 1 & 0 \end{matrix}\right). $$ Now, the number of cycles with $k$ edges will be given by $$ N^{(2)}_k = \left(\begin{matrix}0 & 0 & 0 & 1 \end{matrix}\right) \left(\begin{matrix}0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 2 & 1 & 1 & 0 \end{matrix}\right)^{k-1} \left(\begin{matrix}1 \\ 0 \\ 0 \\ 0 \end{matrix}\right) = \left(\begin{matrix}0 & 0 & 1 \end{matrix}\right) \left(\begin{matrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 0 \end{matrix}\right)^{k-2} \left(\begin{matrix} 1 \\ 1 \\ 2 \end{matrix}\right), $$ where we can eliminate the first row and column of the full transfer matrix because the initial state ($A$) never recurs (i.e., the first row is all zeroes). Note that we are counting the number of ways to go from the initial state to the final state, $D$, in $k-1$ steps. In this case, the vector on the right-hand side is an eigenvector of the (reduced) transfer matrix with eigenvalue $1$, so $$ N^{(2)}_k=\left(\begin{matrix}0 & 0 & 1 \end{matrix}\right) \left(\begin{matrix} 1 \\ 1 \\ 2 \end{matrix}\right) = 2 $$ for any $k \ge 2$. In general, though, we will have $N_k=\sum_i c_i \lambda_i^{k-2}$, where the $\lambda_i$ are eigenvalues of the reduced transfer matrix.

---

The $r=2$ case can be made even simpler by noting that the set of states is symmetric under exchange of red and blue ($A$ and $D$ are themselves symmetric, and $B$ and $C$ are symmetric images of each other), so we can treat mirror pairs as single states. The transitions are then: $A$ to $D$ (two ways), $A$ to $B/C$ (two ways), $B/C$ to $B/C$, and $B/C$ to $D$. So $$ N^{(2)}_k = \left(\begin{matrix}0 & 0 & 1 \end{matrix}\right) \left(\begin{matrix}0 & 0 & 0 \\ 2 & 1 & 0 \\ 2 & 1 & 0 \end{matrix}\right)^{k-1} \left(\begin{matrix}1 \\ 0 \\ 0 \end{matrix}\right) = \left(\begin{matrix}0 & 1 \end{matrix}\right) \left(\begin{matrix} 1 & 0 \\ 1 & 0 \end{matrix}\right)^{k-2} \left(\begin{matrix} 2 \\ 2 \end{matrix}\right) \\ = \left(\begin{matrix}0 & 1 \end{matrix}\right)\left(\begin{matrix} 2 \\ 2 \end{matrix}\right) = 2. $$ This additional simplification, though hardly necessary for $r=2$, will come in handy for $r=3$.

---

For a less trivial application of the transfer matrix approach (but still not the full $r=3$ case), I considered the asymmetric model where each jump is uniformly drawn from $\{-2,-1,1,2,3\}$. The states in this case are:

The legal transitions are: $A$ to $(B,C,D,E,H)$ (and $A$ to $H$ can happen two ways), $B$ to $(C,D,H)$ (two way from $B$ to $H$), $C$ to $(D,H)$, $D$ to $(B,H)$, $E$ to $(F,G)$, $F$ to $G$, and $G$ to $H$. So the number of cycles with $k$ edges is given by $$ \left(\begin{matrix}0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}\right)\left(\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 1 & 0 & 0\\ 2 & 1 & 1 & 0 & 0 & 1 & 0\\ \end{matrix}\right)^{k-2} \left(\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 2 \end{matrix}\right). $$ Using the Jordan decomposition of the reduced transfer matrix, this is $$ \left(\begin{matrix}1 & 0 & 0 & 0 & 1 & 1 & 1 \end{matrix}\right)\left(\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & \nu_1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & \nu_2 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & \nu_2^{*} \end{matrix}\right)^{k-2}\left(\begin{matrix} -1 \\ 0 \\ 1 \\ 1 \\ c_1 \\ c_2 \\ c_2^{*} \end{matrix}\right) \\ =c_1 \nu_1^{k-2} + c_2 \nu_2^{k-2} + c_2^{*} (\nu_2^{*})^{k-2} - \delta_{k,2} + \delta_{k,4} + \delta_{k,5}, $$ where $\nu_1=1.32472$, $\nu_2=-0.662359 - 0.56228 i$, $c_1=2.945975$, and $c_2=0.0270124 + 0.118443 i$. Then the probability of safe return to $0$ is given by $$ P^{(3,2)}=\sum_{k=2}^{\infty}\frac{kN_k^{(3,2)}}{5^k}=-\frac{2}{5^2}+\frac{4}{5^4}+\frac{5}{5^5}+\sum_{i} c_i \sum_{k=2}^{\infty}\frac{k \nu_i^{k-2}}{5^k} \\ = -\frac{9}{125} + \sum_i \frac{c_i(10-\nu_i)}{5(5-\nu_i)^2} = -0.072 + 0.378409 + 2\cdot 0.00289355 \\ = 0.3121961. $$ For comparison, in a simple simulation of $10^8$ trials (running each trial for at most $1000$ jumps), $31218647$ asymmetric jumpers returned safely to the origin. This gives an estimate of $0.31219 \pm 0.00006$ for the probability; i.e., the simulation agrees perfectly with the matrix calculation above.

---

Finally, for $r=3$ we have the following set of states:

Several pairs of states are related by red-blue exchange symmetry (e.g., $B$ and $B'$). Using this symmetry, we can write the transfer matrix in terms of symmetric states only (e.g., $B/B'$), as described earlier for the $r=2$ case. The transitions out of unprimed states are:

• $A$ to $(B,B',C,C',D,H(\times 3))$
• $B$ to $(B',C,C',E,H(\times 2))$
• $C$ to $(B',H)$
• $D$ to $(F,F',G,G')$
• $E$ to $(F',G')$
• $F$ to $G$
• $G$ to $(C,H)$.

So

$$ N_k^{(3)} = \left(\begin{matrix}0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}\right)\left(\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0\\ 2 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 2 & 1 & 0 & 0 & 0\\ 0 & 0 & 2 & 1 & 1 & 0 & 0\\ 2 & 1 & 0 & 0 & 0 & 1 & 0\\ \end{matrix}\right)^{k-2} \left(\begin{matrix} 2 \\ 2 \\ 1 \\ 0 \\ 0 \\ 0 \\ 3 \end{matrix}\right). $$ This sequence begins with $3,6,14,30,62,130,\ldots$. After diagonalizing the matrix, we arrive at $$ N_k^{(3)}=\delta_{k,2}+\left(\begin{matrix}1 & 1 & 1 & 1 \end{matrix}\right)\left(\begin{matrix} \nu_1 & 0 & 0 & 0 \\ 0 & \nu_2 & 0 & 0 \\ 0 & 0 & \nu_3 & 0\\ 0 & 0 & 0 & \nu_3^{*} \end{matrix}\right)^{k-2}\left(\begin{matrix} c_1 \\ c_2 \\ c_3 \\ c_3^{*} \end{matrix}\right)=\delta_{k,2} + \sum_i c_i \nu_i^{k-2}, $$ where $$ \nu_1 = -0.716673 \\ \nu_2 = 2.10692 \\ \nu_3 = 0.304877 - 0.754529 i \\ c_1 = -0.188335 \\ c_2 = 3.136179 \\ c_3 = -0.4739206 - 0.3006352 i. $$ Finally, the desired probability is $$ P^{(3)} = \sum_{k=2}^{\infty}\frac{kN_k^{(3)}}{6^k}=\frac{1}{18}+\sum_i \frac{c_i(12-\nu_i)}{6(6-\nu_i)^2}=0.325873. $$ Checking by simulation for $10^8$ trials yields an estimate of $0.32587 \pm 0.00006$, wholly consistent with this result.

---

Automating the process

One can do all of the following by making a number of formalizations. It is advantageous to mechanize the process before proceeding to larger cases; in particular, we will represent a state as a triple $(X,Y,P)$ where $X$ is the set of remaining ranges of rightward (red) edges, $Y$ is the set of leftward (blue) edges, and $P$ is a partition of $X\cup Y$ representing which edges have been connected (noting that if $x=y$ then the edges represented by $x\in X$ and $y\in Y$ originated together and are clearly connected). We will say $(X',Y',P')$ is an $n$-translate of $(X,Y,P)$ if we might see the former after moving our "window" $n$ steps to the right. For convenience, define $$m=\min(X\cup Y)$$ $$S-n=\{s-n:s\in S\}$$ and, because the relations are not conducive to standard notation, I will leave to the reader the problem of relating $P'$ and $P$. Then, we can have the following situations.

• Birth: In the state where the node in question has two rightward edges passing from it. We require: $$X'=X-n\cup \{r\}$$ $$Y'=Y-n\cup \{r\}$$ We will consider $r$ to be its own connectedness class in $P'$, and otherwise just shift everything.

• Right-Continuation: This is the state where the node receives a rightward edges and also outputs one, we need that for some $c\in X-n$ we have: $$X'=X-n\cup\{r\}\setminus\{c\}$$ $$Y'=Y-n$$ The partition will essentially shift and add $r$ to the equivalence class of $c$.

• Left-Continuation: This is where a node receives and produces a leftward edge. Flop $X$ and $Y$ in the above definition.

• Death: This is where a node is a local maximum, receiving two edges. We need that $$X'=X-n\setminus\{c_x\}$$ $$Y'=Y-n\setminus\{c_y\}$$ where $c_x$ and $c_y$ are appropriate members of $X-n$ and $Y-n$ respectively. Neither $X'$ nor $Y'$ may contain $0$. The equivalence classes representing $c_x$ and $c_y$ will be merged. If $c_x$ and $c_y$ were the last remaining representatives of their equivalence class, then the remaining edges were not connected to them; this transition is invalid unless $X'=Y'=\{\}$.

Then, in the matrix, the number of ways to transition from one state to another is the number of $n$'s such that the latter is an $n$-translate of the former. My code works by generating every conceivable state - i.e. every pair $(X,Y,P$) where $|X|=|Y|$ and $P$ is a partition of $X\cup Y$. Some of these are inaccessible from the starting state or cannot access the ending state, but I did not write code to prune such states away. I also did not take advantage of the symmetry $(X,Y,P)\rightarrow(Y,X,P)$. Either would likely lead to big increases in efficiency, allowing the computation of more values $P^{(r)}$.

It is worthy of note that $$\sum_{k=2}^{\infty}a\cdot \frac{kM^{k-1}}{2k}\cdot b=a\cdot\left(\sum_{k=2}^{\infty}\frac{kM^{k-1}}{2r}\right)\cdot b$$ by linearity, meaning we can first use the identity that $$\sum_{k=2}^{\infty}\frac{kM^{k-1}}{(2r)^k}=\frac{1}{4r^2}(2I-\frac{1}{2r}M)\cdot M\cdot(\frac{1}{2r}M-I)^{-2}$$ which is easily derived by noting that $M$ acts, for these purposes, just like a real number with $|M|<2r$ as $M$ must have no eigenvalues of absolute value $2r$ or more (given that there are only $(2r)^k$ paths of length $k$, whereas there are about $k\lambda^k$ cycles of length $k$ with identified starting point where $\lambda$ is the largest eigenvalue of $M$). Then, we can take the transfer matrix, directly compute the infinite sum as above, and extract the desired coefficient. It should be noted that this will always yield a rational answer. In particular, we receive: $$P^{(1)}=\frac{1}2$$ $$P^{(2)}=\frac{7}{18}$$ $$P^{(3)}=\frac{4368595}{13405842}\approx 0.325872$$ $$P^{(4)}=\frac{33373525946827013707062414432976}{117177232862732965149684560993569}\approx 0.284812$$

Mathematica code may be found in this revision. It may be noted that the methods may be modified easily to handle asymmetric cases or cases with non-uniform probability - essentially, instead of using our transfer matrix as a count, we can use it to measure the probability of a cycle occurring given that we start on a given point of it.

Answer 2

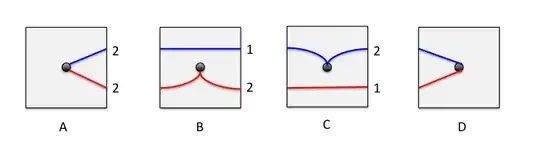
Here is another approach, which involves a lot of elementary computations. The key is similarity. In the case of steps up to size two, this works in the following way: Let $P(i_1,i_2,\dots,i_k)$ denote the probability to stop at zero after you went through $i_1,i_2,\dots,i_k$.

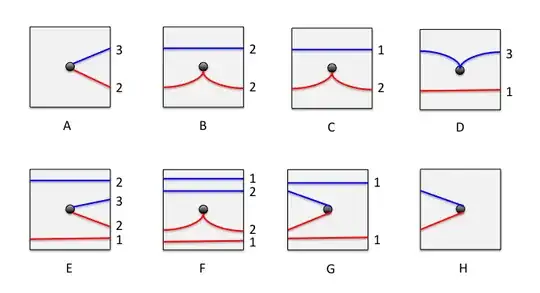
Then the probability you search is $$ P=\frac 14(P(-2)+P(-1)+P(1)+P(2)). $$ By symmetry (or the first type of similarity) you have $$ P=\frac 12(P(1)+P(2)). $$ Now $P(1)=\frac 14(P(1,-1)+1+P(1,2)+P(1,3))$ where $1=P(1,0)$.

Next compute $$ P(1,-1)=\frac 14(P(1,-1,-3)+P(1,-1,-2)+1). $$ Clearly $P(1,-1,-2)=\frac 14$ since the only chance to stop at zero after that path is to go directly to zero, with probability $1/4$. But the path $P(1,-1,-3)$ is similar to $P(1,-1)$ and we see that $$ P(1,-1,-3)=\frac 14 P(1,-1). $$ We will prove the method of similarity only here, and then use it freely: There is a bijection between the paths going after $(1,-1)$ to zero and the paths going after $(1,-1,-3)$ to zero, the bijection assigns to the path $(1,-1,n_1,\dots,n_k)$ with $n_k=0$ the path $(1,-1,-3,n_1-2,\dots,n_k-2,0)$. Since the latter path has a probability $\frac 14$ less to occur than the former, we obtain the factor $\frac 14$ relating $P(1,-1,-3)$ and $P(1,-1)$.

So we have $$ 4P(1,-1)=P(1,-1,-3)+P(1,-1,-2)+1=\frac 14 P(1,-1)+\frac 14+1, $$ from which it follows that $P(1,-1)=1/3$.

Now $P(1,2)=\frac 14$ since the only chance to stop at zero after that path is to go directly to zero, with probability $1/4$, and $P(1,3)$ is similar to $P(1,-1)$ with $P(1,3)=\frac 14 P(1,-1)=1/{12}$.

So $$ P(1)=\frac 14(P(1,-1)+1+P(1,2)+P(1,3))=\frac 14\left(\frac 13+1+\frac 14+\frac{1}{12}\right)=\frac{5}{12}. $$

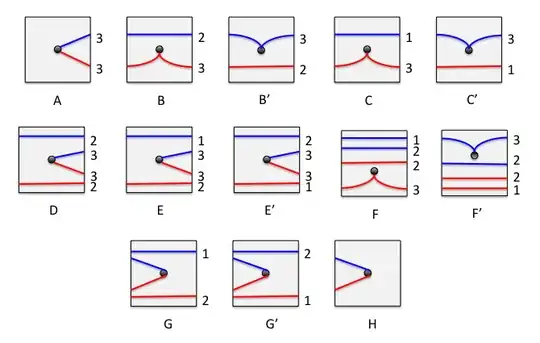
Finally compute $$ P(2)=\frac 14(1+P(2,1)+P(2,3)+P(2,4)). $$ Note that $P(2,3)=\frac 14 P(2,3,1)=\frac 14 P(2,1)$, since the only chance is to jump directly to 1; the second equality follows by similarity. We also have $$ P(2,4)= P(1,3)P(2,4,3,1)= P(1,3)P(2,1)=\frac{1}{12}P(2,1), $$ by similarity, where a path after $(2,4)$ is split into one path going to 1 (which gives by similarity $P(1,3)$) and the other part corresponds to a path going to zero after $(2,1)$.

Hence $$ P(2)=\frac 14(1+P(2,1)+P(2,3)+P(2,4))=\frac 14\left(1+P(2,1)\left(1+\frac 14+\frac 1{12}\right)\right)=\frac 14\left(1+\frac 43 P(2,1)\right). $$ So we have to compute $P(2,1)=\frac 14(P(2,1,-1)+1+P(2,1,3))$. But $P(2,1,3)=0$ and by similarity $P(2,1,-1)=P(1,-1)=1/3$. So we arrive at $$ P(2,1)=\frac 14\left(\frac 13+1\right)=\frac 13, $$ and so $$ P(2)=\frac 14\left(1+\frac 43 P(2,1)\right)=\frac{13}{36}. $$ Finally $P=\frac 12(P(1)+P(2))=\frac 12(\frac{5}{12}+\frac{13}{36})=\frac{7}{18}$, which coincides with the value you have found.

This method can be applied in the case where the steps are of maximal length three, but there are much more cases to consider. For example, we try to compute $P(-1,-2,1)$: $$ P(-1,-2,1)=\frac 16\left(1+P(-1,-2,1,2)+P(-1,-2,1,3)+P(-1,-2,1,4)\right). $$ By similarity we have $P(-1,-2,1,3)=\frac 16(1+P(-1,-2,1))$. We also have $$ P(-1,-2,1,2)=\frac 16\left(1+P(-1,-2,1,2,3)+P(-1,-2,1,2,4)+P(-1,-2,1,2,5)\right) $$ $$ =\frac 16\left(1+\frac 16+\frac 16 P(-1,-2,1)+P(-1,-2,1,2,5)\right). $$ We can expand $P(-1,-2,1,2,5)$ and the only term that causes trouble is $P(-1,-2,1,2,5,8)$. In general, we need a nice expression for all terms $P(-1,-2,1,2,5,8,\dots,2+3k)$. Similarly in the expansion of $P(-1,-2,1,4)$ we need a nice expression of the term $P(-1,-2,1,4,7,\dots, 1+3k)$. I think, if you express $P(-1,-2,1,4,7,\dots, 1+3k)$ in terms of $P(-1,-2,1,4,7,\dots, 1+3k,4+3k)$, and use that $\lim P(-1,-2,1,4,7,\dots, 1+3k)=0$, one could work out a formula for these terms and similarly for $P(-1,-2,1,2,5,8,\dots,2+3k)$.