Twilight Zelda Guardian Puzzle : Shortest Path (UPDATE: ADDED RULES)

Question

I'm playing a video game right now and in it is a puzzle (see here). There are solutions to solving it (see here) on the Internet, but I'd like to know if this path is the shortest path (least amount of moves) possible to solve the puzzle.

The rules of the game are clear from the video. There is a grid of nodes. The border nodes are bounded with limited path choices. There are three moving bodies. The main one chooses a path that reflects the path choices of the other two. The aim is to guide the other two to land on certain nodes at the same time.

IMPORTANT RULES:

If the guardians face each other and Link, the player, moves in a way to make them collide they, in effect, stay in the same position and Link keeps his move: youtube.com/watch?v=ZNnSwc0w1oE#t=4m58s

Top-guardian-Link conga allowed: youtube.com/watch?v=oUh88KsZYCc#t=3m53s – Liz Wesley 21 mins ago

The game ends if the player jumps on a square that a guardian is set to jump on at the same time: youtube.com/watch?v=ZNnSwc0w1oE#t=2m55s

I'm seeking a shortest path proof based on this game's rules. Any help would be appreciated.

It is important to note that the top guardian moves in the opposite direction as link and the bottom guardian mimics Link's direction.

Daniel Wagner's 12-step Haskell Solution:

enter image description here

Guardian Path Overlay:

enter image description here

What happens if the guardians jump into each other or into the player? — Samuel, Apr 21 '15 at 23:55
If any two of the three face each other (node-to-node *-><-*) and move towards each other they stay in the same place. In other words, jumping into each other is an illegal move. I don't know what something like *->*<-* would do. I can't go back because I already solved it. My assumption is that if they both try to hop on the same node the main player will hop on it and the guardian will remain static or both will be unable to move. Either way this can be built in to your model as two separate cases. Calculate the results for the first theory, then the results for the second. — Liz Wesley, Apr 22 '15 at 00:12
How about we agree to say that any move that would have any of the guardians or the player collide or jump through each other is an illegal move? If someone else who has played the game and knows otherwise they may say so and we can change it. — Samuel, Apr 22 '15 at 00:18
I also observe that your specification, "if any two of the three move towards each other they stay in the same place" is in conflict with your explanatory "in other words jumping into each other is an illegal move". Legal moves that leave some entities in the same place are not the same as moves which simply can't be chosen. — Daniel Wagner, Apr 22 '15 at 02:00
It's also important to know what happens when two guardians face each other and the player is behind the bottom guardian (same direction guardian). This is special case for the conga, as it would be allowed if the top guardian was not in front of the bottom guardian. — Liz Wesley, Apr 25 '15 at 23:39

Daniel Wagner · Accepted Answer · 2015-04-22T02:34:42.233

Under a few assumptions, I compute that the shortest path requires 12 steps; the player should make the moves ESNNNWWSSSEN. (This is one step shorter than the two solutions you linked to.) The assumptions I made are:

Entities which would step out of the game board do not move.
All three entities step simultaneously.
The player may not make a move which would cause an entity to change their location to one that is currently occupied. (Remaining in place is okay.)
The player may not remain in place.
The player may not make a move which would cause two entities to occupy the same cell.

Below I include a full code listing (in Haskell) which describes the game and performs A* search as implemented by the astar package to find a minimal path. As a heuristic, we consider the two ways of pairing guardians and goal cells; in each pairing, we compute the Manhattan distance of the guardian that has farther to walk, then take the smaller maximum distance from these two pairings. This is certainly admissible, since we must take at least as many steps as the guardians are away from their goal cells. Assumption (1) is encoded in stepValid; (2) in unsafeMove; (3)-(5) in movementIsValid. Shorter solutions may be possible if these assumptions are incorrect.

import Data.List
import Data.Graph.AStar
import Data.Ord
import Data.Set (Set, fromList)

type Position = (Int, Int)
data Direction = N | E | S | W deriving (Eq, Ord, Read, Show, Bounded, Enum)

allDirections :: [Direction]
allDirections = [N, E, S, W]

mirror :: Direction -> Direction
mirror N = S
mirror E = W
mirror S = N
mirror W = E

dx, dy :: Direction -> Int
dx E =  1
dx W = -1
dx _ =  0
dy N =  1
dy S = -1
dy _ =  0

step :: Direction -> Position -> Position
step d (x, y) = (x + dx d, y + dy d)

data Configuration = Configuration
    { valid :: [Position]
    , goalA :: Position
    , goalB :: Position
    } deriving (Eq, Ord, Read, Show)

data State = State
    { player         :: Position
    , guardianSame   :: Position
    , guardianMirror :: Position
    } deriving (Eq, Ord, Read, Show)

stepValid :: Configuration -> Direction -> Position -> Position
stepValid c d p
    | p' `elem` valid c = p'
    | otherwise = p
    where p' = step d p

unsafeMove :: Configuration -> Direction -> State -> State
unsafeMove c d State { player = p, guardianSame = gs, guardianMirror = gm } = State
    { player         = stepValid c d p
    , guardianSame   = stepValid c d gs
    , guardianMirror = stepValid c (mirror d) gm
    }

movementIsValid :: State -> State -> Bool
movementIsValid old new
    =  player         new `notElem`                             oldPositions
    && guardianSame   new `notElem` delete (guardianSame   old) oldPositions
    && guardianMirror new `notElem` delete (guardianMirror old) oldPositions
    && nub newPositions == newPositions
    where
    newPositions = [player new, guardianSame new, guardianMirror new]
    oldPositions = [player old, guardianSame old, guardianMirror old]

movements :: Configuration -> State -> Set State
movements c old = fromList
    [ new
    | d <- allDirections
    , let new = unsafeMove c d old
    , movementIsValid old new
    ]

manhattan :: Position -> Position -> Int
manhattan (x, y) (x', y') = abs (x-x') + abs (y-y')

heuristic :: Configuration -> State -> Int
heuristic c s = min
    (max (manhattan (guardianSame s) (goalA c)) (manhattan (guardianMirror s) (goalB c)))
    (max (manhattan (guardianSame s) (goalB c)) (manhattan (guardianMirror s) (goalA c)))

cost :: State -> State -> Int
cost _ _ = 1

finished :: Configuration -> State -> Bool
finished c s = heuristic c s == 0

data Cell = Player | Goal | GuardianSame | GuardianMirror | Valid
    deriving (Eq, Ord, Read, Show, Bounded, Enum)

label :: String -> [(Position, Cell)]
label board = do
    (y, row)  <- zip [0..] (reverse (lines board))
    (x, char) <- zip [0..] row
    let cell c = [((x, y), c)]
    case char of
        'x' -> cell Valid
        'g' -> cell Goal
        's' -> cell GuardianSame
        'm' -> cell GuardianMirror
        'p' -> cell Player
        _   -> []

parse :: String -> (Configuration, State)
parse board = (Configuration
    { valid = map fst labels
    , goalA = gA
    , goalB = gB
    }, State
    { player         = p
    , guardianSame   = gs
    , guardianMirror = gm
    })
    where
    labels = label board
    (p, Player):(gA, Goal):(gB, Goal):(gs, GuardianSame):(gm, GuardianMirror):_
        = sortBy (comparing snd) labels

(testConfiguration, testState) = parse
    "xx xx\n\
    \xgmgx\n\
    \xxxxx\n\
    \ xpx \n\
    \ xxx \n\
    \  s  \n"

main = case aStar (movements testConfiguration) cost (heuristic testConfiguration) (finished testConfiguration) testState of
    Nothing       -> putStrLn "no solution exists for the test board"
    Just solution -> mapM_ print solution

I made a TIKZ graph of your solution: overleaf.com/2588660pvgwfg — Liz Wesley, Apr 22 '15 at 03:03
Assumption 3 seems to disallow a two-man conga line, which I don't think should be illegal. — Samuel, Apr 22 '15 at 10:20
I agree with what Samuel said, but such a conga would only be allowed for the bottom guardian. — Liz Wesley, Apr 22 '15 at 16:14
@Samuel If somebody can carefully describe the correct set of assumptions, I will be happy to update my answer. But I don't intend to spend a lot of time chasing down myriad variations on this theme, so emphasis on carefully. — Daniel Wagner, Apr 22 '15 at 17:33
@DanielWagner, Samuel is right: https://www.youtube.com/watch?v=oUh88KsZYCc#t=3m53s — Liz Wesley, Apr 24 '15 at 02:09
The game ends if the player jumps on a square that a guardian is set to jump on at the same time: https://www.youtube.com/watch?v=ZNnSwc0w1oE#t=2m55s — Liz Wesley, Apr 24 '15 at 02:23
If the guardians face each other and Link, the player, moves in a way to make them collide they, in effect, stay in the same position and Link keeps his move: https://www.youtube.com/watch?v=ZNnSwc0w1oE#t=4m58s — Liz Wesley, Apr 24 '15 at 02:28
@LizWesley: Nice find! It remains to find out what happens if two guardians jump towards eachother when they are adjacent, or when a guardian and the player jump towards eachother when they are adjacent. A reasonable guess is that it works like it did when they had one square between them, like in the videos you linked. — Samuel, Apr 25 '15 at 11:28
@Samuel, adjacent, same-facing guardians will stay in the same location when the player makes a move, and the player keeps the move. Adjacent, same-facing player-guardian move results in a game restart. — Liz Wesley, Apr 25 '15 at 18:54

score 1 · Answer 2 · answered May 18 '15 at 00:09

I built the game in Mathematica using the rules I think you're trying to accomplish. Here is the code if you have Mathematica:

$\hspace{3cm}$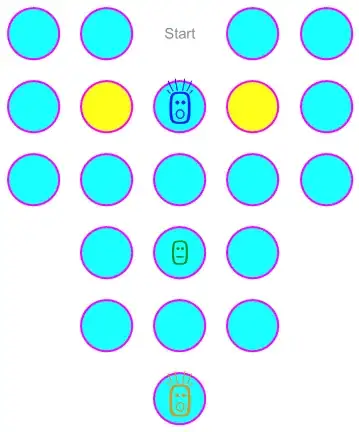 enter image description here

bound = {{2, -1}, {2, 5}, {1, 0}, {3, 0}, {0, 1}, {4, 1}, {0, 2}, {4, 
   2}, {-1, 3}, {5, 3}, {-1, 4}, {5, 4}, {-1, 5}, {5, 5}, {0, 6}, {1, 
   6}, {3, 6}, {4, 6}}

DynamicModule[{pos1 = {x1, y1} = {2, 2}, pos2 = {x2, y2} = {2, 4}, 
  pos3 = {x3, y3} = {2, 0}, message = "Start", 
  DotT = {a2, b2} = {x2, (y2 - 0.51)}, 
  DotL = {a1, b1} = {x1, (y1 + 0.51)}, 
  DotB = {a3, b3} = {x3, (y3 + 0.51)}, Switch = True, Stick = False}, 
 EventHandler[
  Dynamic[Magnify[
    Graphics[{Opacity[0.9], 
      Style[Text[message, {2, 5}], FontFamily -> "Helvetica", Small, 
       Gray, FontSize -> 15], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{0, 5}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{0, 4}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{0, 3}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{1, 5}, .35], Yellow, Disk[{1, 4}, .35], 
      EdgeForm[Directive[Thick, Magenta]], Cyan, Disk[{1, 3}, .35], 
      EdgeForm[Directive[Thick, Magenta]], Cyan, Disk[{3, 5}, .35], 
      Yellow, Disk[{3, 4}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{3, 3}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{4, 5}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{4, 4}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{4, 3}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{1, 1}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{2, 1}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{3, 1}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{1, 2}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{2, 2}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{3, 2}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{2, 0}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{2, 3}, .35], EdgeForm[Directive[Thick, Magenta]], 
      Cyan, Disk[{2, 4}, .35], Darker[Green, 0.5], 
      Style[Text[\[NeutralSmiley], pos1], FontSize -> 36], Blue, 
      Style[Text[\[FreakedSmiley], pos2], FontSize -> 48], Orange, 
      Style[Text[\[FreakedSmiley], pos3], 
       FontSize -> 48]}]]], {"UpArrowKeyDown" :> {message = "", 
     Switch = True, Stick = False, 
     If[(**){x1, y1 + 1} == {x2, y2 - 1} || {x1, y1 + 1} == {x2, 
         y2} || {x1, y1 + 1} == {x3, y3} || {x3, y3 + 1} == {x2, 
         y2 - 1} || {x3, y3 + 1} == {x2, 
         y2}, {Which[{x3, y3 + 1} == {x2, y2 - 1}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1 + 1}}, pos2 = pos2, 
         pos3 = pos3}, {x3, y3 + 1} == {x2, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1 + 1}}, pos2 = pos2, 
         pos3 = pos3}, {x1, y1 + 1} == {x2, y2 - 1}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = 2, y1 = 2}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = 2, y2 = 4}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = 2, y3 = 0}}, 
         message = "Gameover", DotT = {2, (4 - .51)}, 
         DotL = {2, (2 + .51)}, DotB = {2, (0 + .51)}, 
         Switch = False}, {x1, y1 + 1} == {x2, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}}, {x1, 
          y1 + 1} == {x3, y3}, {Which[
          Intersection[
            bound, {{x3, y3 + 1}}] == {{x3, y3 + 1}}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}}, {x3, 
            y3 + 1} == {x2, y2 - 1}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = 2, y1 = 2}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = 2, y2 = 4}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = 2, y3 = 0}}, 
           message = "Gameover", DotT = {2, (4 - .51)}, 
           DotL = {2, (2 + .51)}, DotB = {2, (0 + .51)}, 
           Switch = False}, 
          Intersection[
            bound, {{x3, y3 + 1}}] != {{x3, y3 + 1}}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1 + 1}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2 - 1}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = x3, 
                y3 = y3 + 
                  1}}}]}]}, {If[(*Test if next move out of bound.*)
        Intersection[bound, {{x1, y1 + 1}}] == {{x1, y1 + 1}}, {pos1 =
           pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, Stick = True}, 
        pos1 = pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1 + 1}}], 
       If[(*Test if next move out of bound.*)
        Intersection[bound, {{x2, y2 - 1}}] == {{x2, y2 - 1}}, 
        pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
        If[Stick == True, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2 - 1}}]], 
       If[(*Test if next move out of bound.*)
        Intersection[bound, {{x3, y3 + 1}}] == {{x3, y3 + 1}}, 
        pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}, 
        If[Stick == True, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3 + 1}}]]}], 
     If[Switch == True, {DotT = {a2 = x2, b2 = y2 - .51}, 
       DotL = {a1 = x1, b1 = y1 + .51}, 
       DotB = {a3 = x3, b3 = y3 + .51}}], Switch = True, 
     If[{x2, y2} == {1, 4} && {x3, y3} == {3, 4} || {x3, y3} == {1, 
          4} && {x2, y2} == {3, 4}, message = "Win"]}, 
   "DownArrowKeyDown" :> {message = "", Switch = True, Stick = False, 
     If[(**){x1, y1 - 1} == {x2, y2 + 1} || {x1, y1 - 1} == {x2, 
         y2} || {x1, y1 - 1} == {x3, y3} || {x3, y3 - 1} == {x2, 
         y2 + 1} || {x3, y3 - 1} == {x2, 
         y2}, {Which[{x3, y3 - 1} == {x2, y2 + 1}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1 - 1}}, pos2 = pos2, 
         pos3 = pos3}, {x3, y3 - 1} == {x2, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1 - 1}}, pos2 = pos2, 
         pos3 = pos3}, {x1, y1 - 1} == {x2, y2 + 1}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = 2, y1 = 2}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = 2, y2 = 4}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = 2, y3 = 0}}, 
         message = "Gameover", DotT = {2, (4 - .51)}, 
         DotL = {2, (2 + .51)}, DotB = {2, (0 + .51)}, 
         Switch = False}, {x1, y1 - 1} == {x2, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}}, {x1, 
          y1 - 1} == {x3, y3}, {Which[
          Intersection[
            bound, {{x3, y3 - 1}}] == {{x3, y3 - 1}}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}}, {x3, 
            y3 - 1} == {x2, y2 + 1}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = 2, y1 = 2}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = 2, y2 = 4}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = 2, y3 = 0}}, 
           message = "Gameover", DotT = {2, (4 - .51)}, 
           DotL = {2, (2 + .51)}, DotB = {2, (0 + .51)}, 
           Switch = False}, 
          Intersection[
            bound, {{x3, y3 - 1}}] != {{x3, y3 - 1}}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1 - 1}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2 + 1}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = x3, 
                y3 = y3 - 
                  1}}}]}]}, {If[(*Test if next move out of bound.*)
        Intersection[bound, {{x1, y1 - 1}}] == {{x1, y1 - 1}}, {pos1 =
           pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, Stick = True}, 
        pos1 = pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1 - 1}}], 
       If[(*Test if next move out of bound.*)
        Intersection[bound, {{x2, y2 + 1}}] == {{x2, y2 + 1}}, 
        pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
        If[Stick == True, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2 + 1}}]], 
       If[(*Test if next move out of bound.*)
        Intersection[bound, {{x3, y3 - 1}}] == {{x3, y3 - 1}}, 
        pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}, 
        If[Stick == True, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3 - 1}}]]}], 
     If[Switch == True, {DotT = {a2 = x2, b2 = y2 + .51}, 
       DotL = {a1 = x1, b1 = y1 - .51}, 
       DotB = {a3 = x3, b3 = y3 - .51}}], Switch = True, 
     If[{x2, y2} == {1, 4} && {x3, y3} == {3, 4} || {x3, y3} == {1, 
          4} && {x2, y2} == {3, 4}, message = "Win"]}, 
   "LeftArrowKeyDown" :> {message = "", Switch = True, Stick = False, 
     If[(**){x1 - 1, y1} == {x2 + 1, y2} || {x1 - 1, y1} == {x2, 
         y2} || {x1 - 1, y1} == {x3, y3} || {x3 - 1, y3} == {x2 + 1, 
         y2} || {x3 - 1, y3} == {x2, 
         y2}, {Which[{x3 - 1, y3} == {x2 + 1, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1 - 1, y1 = y1}}, pos2 = pos2, 
         pos3 = pos3}, {x3 - 1, y3} == {x2, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1 - 1, y1 = y1}}, pos2 = pos2, 
         pos3 = pos3}, {x1 - 1, y1} == {x2 + 1, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = 2, y1 = 2}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = 2, y2 = 4}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = 2, y3 = 0}}, 
         message = "Gameover", DotT = {2, (4 - .51)}, 
         DotL = {2, (2 + .51)}, DotB = {2, (0 + .51)}, 
         Switch = False}, {x1 - 1, y1} == {x2, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}}, {x1 - 1, 
          y1} == {x3, y3}, {Which[
          Intersection[
            bound, {{x3 - 1, y3}}] == {{x3 - 1, y3}}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}}, {x3 - 1, 
            y3} == {x2 + 1, y2}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = 2, y1 = 2}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = 2, y2 = 4}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = 2, y3 = 0}}, 
           message = "Gameover", DotT = {2, (4 - .51)}, 
           DotL = {2, (2 + .51)}, DotB = {2, (0 + .51)}, 
           Switch = False}, 
          Intersection[
            bound, {{x3 - 1, y3}}] != {{x3 - 1, y3}}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = x1 - 1, y1 = y1}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = x2 + 1, y2 = y2}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = x3 - 1, 
                y3 = y3}}}]}]}, {If[(*Test if next move out of bound.*)
        Intersection[bound, {{x1 - 1, y1}}] == {{x1 - 1, y1}}, {pos1 =
           pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, Stick = True}, 
        pos1 = pos1 /. {{x1, y1} -> {x1 = x1 - 1, y1 = y1}}], 
       If[(*Test if next move out of bound.*)
        Intersection[bound, {{x2 + 1, y2}}] == {{x2 + 1, y2}}, 
        pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
        If[Stick == True, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2 + 1, y2 = y2}}]], 
       If[(*Test if next move out of bound.*)
        Intersection[bound, {{x3 - 1, y3}}] == {{x3 - 1, y3}}, 
        pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}, 
        If[Stick == True, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3 - 1, y3 = y3}}]]}], 
     If[Switch == True, {DotT = {a2 = x2 + .51, b2 = y2}, 
       DotL = {a1 = x1 - .51, b1 = y1}, 
       DotB = {a3 = x3 - .51, b3 = y3}}], Switch = True, 
     If[{x2, y2} == {1, 4} && {x3, y3} == {3, 4} || {x3, y3} == {1, 
          4} && {x2, y2} == {3, 4}, message = "Win"]}, 
   "RightArrowKeyDown" :> {message = "", Switch = True, Stick = False,
      If[(**){x1 + 1, y1} == {x2 - 1, y2} || {x1 + 1, y1} == {x2, 
         y2} || {x1 + 1, y1} == {x3, y3} || {x3 + 1, y3} == {x2 - 1, 
         y2} || {x3 + 1, y3} == {x2, 
         y2}, {Which[{x3 + 1, y3} == {x2 - 1, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1 + 1, y1 = y1}}, pos2 = pos2, 
         pos3 = pos3}, {x3 + 1, y3} == {x2, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1 + 1, y1 = y1}}, pos2 = pos2, 
         pos3 = pos3}, {x1 + 1, y1} == {x2 - 1, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = 2, y1 = 2}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = 2, y2 = 4}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = 2, y3 = 0}}, 
         message = "Gameover", DotT = {2, (4 - .51)}, 
         DotL = {2, (2 + .51)}, DotB = {2, (0 + .51)}, 
         Switch = False}, {x1 + 1, y1} == {x2, y2}, {pos1 = 
          pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}}, {x1 + 1, 
          y1} == {x3, y3}, {Which[
          Intersection[
            bound, {{x3 + 1, y3}}] == {{x3 + 1, y3}}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 

           pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}}, {x3 + 1, 
            y3} == {x2 - 1, y2}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = 2, y1 = 2}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = 2, y2 = 4}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = 2, y3 = 0}}, 
           message = "Gameover", DotT = {2, (4 - .51)}, 
           DotL = {2, (2 + .51)}, DotB = {2, (0 + .51)}, 
           Switch = False}, 
          Intersection[
            bound, {{x3 + 1, y3}}] != {{x3 + 1, y3}}, {pos1 = 
            pos1 /. {{x1, y1} -> {x1 = x1 + 1, y1 = y1}}, 
           pos2 = pos2 /. {{x2, y2} -> {x2 = x2 - 1, y2 = y2}}, 
           pos3 = pos3 /. {{x3, y3} -> {x3 = x3 + 1, 
                y3 = y3}}}]}]}, {If[(*Test if next move out of bound.*)
        Intersection[bound, {{x1 + 1, y1}}] == {{x1 + 1, y1}}, {pos1 =
           pos1 /. {{x1, y1} -> {x1 = x1, y1 = y1}}, Stick = True}, 
        pos1 = pos1 /. {{x1, y1} -> {x1 = x1 + 1, y1 = y1}}], 
       If[(*Test if next move out of bound.*)
        Intersection[bound, {{x2 - 1, y2}}] == {{x2 - 1, y2}}, 
        pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
        If[Stick == True, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2, y2 = y2}}, 
         pos2 = pos2 /. {{x2, y2} -> {x2 = x2 - 1, y2 = y2}}]], 
       If[(*Test if next move out of bound.*)
        Intersection[bound, {{x3 + 1, y3}}] == {{x3 + 1, y3}}, 
        pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}, 
        If[Stick == True, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3, y3 = y3}}, 
         pos3 = pos3 /. {{x3, y3} -> {x3 = x3 + 1, y3 = y3}}]]}], 
     If[Switch == True, {DotT = {a2 = x2 - .51, b2 = y2}, 
       DotL = {a1 = x1 + .51, b1 = y1}, 
       DotB = {a3 = x3 + .51, b3 = y3}}], Switch = True, 
     If[{x2, y2} == {1, 4} && {x3, y3} == {3, 4} || {x3, y3} == {1, 
          4} && {x2, y2} == {3, 4}, message = "Win"]}}]]

Reproducing the game itself does not answer the question of what the shortest path is. — epimorphic, May 18 '15 at 00:26

Twilight Zelda Guardian Puzzle : Shortest Path (UPDATE: ADDED RULES)

IMPORTANT RULES:

Daniel Wagner's 12-step Haskell Solution:

Guardian Path Overlay:

2 Answers2

Linked