What is the solid angle at a vertex in a snub cube?

Question

I was able to find or derive an expression for most other Platonic or Archimedean solids, but for the snub cube I was not able to find a value nor find an expression anywhere.

Answer 1

There is a general expression of the solid angle subtended by the snub cube at any of its $24$ vertices is given by the general expression $$\boxed{\Omega=8\sin^{-1}\left(\frac{(2x-1)\sqrt{3x^2-1}}{\sqrt{3}(4x^2-1)}\right)+2\sin^{-1}\left(\frac{(2x-1)\sqrt{2x^2-1}}{4x^2-1}\right) \space sr}$$ where, $x$ is a parametric variable of an 8th degree polynomial obtained from HCR's Theory of Polygon, given as follows $$128x^8-352x^6+256x^4-72x^2+7=0\ \ \quad \forall \ x>1$$ After $5$ successive iterations using Newton-Raphson's method, the value of $x$ can be fairly approximated as follows
$x\approx 1.343713374$

Now, substituting the above value of $x$, one should get the approximate value of solid angle subtended by the snub cude at any of its 24 vertices ( all lying on the spherical surface) as follows

$$\Omega=\left.8\sin^{-1}\left(\frac{(2x-1)\sqrt{3x^2-1}}{\sqrt{3}(4x^2-1)}\right)+2\sin^{-1}\left(\frac{(2x-1)\sqrt{2x^2-1}}{4x^2-1}\right)\right|_{x\approx 1.343713374} \\ \approx 3.589629551 \space sr$$

For solid angles subtended by all the Archimedean solids, kindly go through Table of solid angles subtended by Archimedean solids at their vertices by HCR

Answer 2

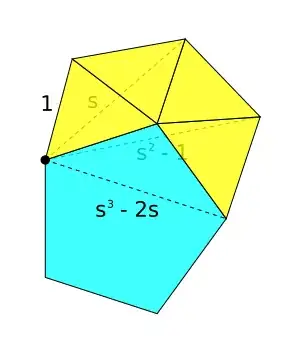
I'll derive the angles for the snub dodecahedron with edge length $1$. For the snub cube, just replace $\varphi=(1+\sqrt5)/2$ with $\varphi=\sqrt2$. (Replace "regular pentagon" with "square", etc.)

Since the polyhedron is vertex-transitive, all vertices are on a sphere, whose centre is the average of the vertices. Since the edge lengths are all equal, all vertices adjacent to one vertex are on another sphere, whose radius is the edge length. The intersection of two spheres is a circle. And a circle is contained in a plane. Thus, the vertices adjacent to one vertex form a planar polygon inscribed in a circle. In fact it's an irregular pentagon; four edges are $1$, and the fifth edge is $\varphi$ (the diagonal of a regular pentagon).

Ignoring that fifth edge for the moment, we have a chain of four equal line segments with three equal angles $\theta$ between them. Let $z^2=e^{i(\pi-\theta)}=-\cos\theta+i\sin\theta$ be the complex number that rotates one segment to the next segment. If the complex plane is oriented such that one end of the chain is $0+0i$ and the next vertex is $1+0i$, then the vertices of the chain are

$$0,\quad1,\quad1+z^2,\quad1+z^2+z^4,\quad1+z^2+z^4+z^6.$$

Let $s=|1+z^2|=z^{-1}+z$ be the short diagonal of the chain. It follows that the other two diagonals are

$$|1+z^2+z^4|=z^{-2}+1+z^2=(z^{-1}+z)^2-1=s^2-1$$

and

$$|1+z^2+z^4+z^6|=z^{-3}+z^{-1}+z+z^3=(z^{-1}+z)^3-2(z^{-1}+z)=s^3-2s.$$

(We didn't need to use complex numbers; you could find a different way to derive these expressions for the diagonal lengths.)

Incorporating the fifth edge, we get an equation that determines $s$:

$$s^3-2s=\varphi.$$

Now let $\alpha$ be the dihedral angle between two triangular faces. Since the altitude of a regular triangle is $\sqrt3/2$, the law of cosines gives

$$\cos\alpha=\frac{(\sqrt3/2)^2+(\sqrt3/2)^2-s^2}{2(\sqrt3/2)(\sqrt3/2)}=1-\tfrac23s^2.$$

And let $\beta$ be the dihedral angle between a triangular and a pentagonal face. Consider the irregular tetrahedron with edges $s^3-2s,\;s^2-1,\;1,\;1,\;1,\;1$. The angle $\phi$ in the triangle with edges $s^2-1,\;1,\;1$ is also given by the law of cosines: $\cos\phi=(1^2+1^2-(s^2-1)^2)/(2(1)(1))=\tfrac12+s^2-\tfrac12s^4$. The angle in a regular triangle is of course $60^\circ$, with $\cos60^\circ=\tfrac12$. The angle in a regular pentagon is $108^\circ$, with $\cos108^\circ=1-\tfrac12\varphi^2$. Then the spherical law of cosines can be applied to a small sphere centred on the tetrahedron's vertex with edges $1,\;1,\;1$:

$$\cos\beta=\frac{\cos\phi-\cos60^\circ\cos108^\circ}{\sin60^\circ\sin108^\circ}=\frac{\tfrac12+s^2-\tfrac12s^4-\tfrac12(1-\tfrac12\varphi^2)}{\tfrac{\sqrt3}2\sqrt{1-(1-\tfrac12\varphi^2)^2}}$$ $$=\frac{4s^2-2s^4+\varphi^2}{\sqrt3\sqrt{4\varphi^2-\varphi^4}}=\frac{-2\varphi s+\varphi^2}{\sqrt3\,\varphi\sqrt{4-\varphi^2}}=\frac{\varphi-2s}{\sqrt{12-3\varphi^2}}.$$

Finally, the solid angle $\Omega$ is the area of the spherical pentagon gotten by intersecting the polyhedron with a small sphere centred on the vertex:

$$\Omega=3\alpha+2\beta-3\pi.$$

---

Here are the numerical values. I take radians and steradians to be the default units, but degrees can be used secondarily: $1^\circ=\tfrac{\pi}{180}=\tfrac{\pi}{180}\text{rad}=\tfrac{\pi}{180}\text{sr}$. So a whole sphere is $4\pi=720^\circ$. The values on the left are for the snub dodecahedron, and the values on the right are for the snub cube.

$$\varphi=\quad1.6180339887,\quad1.4142135624$$ $$s=\quad1.71556149969736783,\quad1.68501832488972093$$ $$\alpha=\quad2.8654006883\text{ rad},\quad2.6744480835\text{ rad} \\ \quad=\quad164.17536606^\circ,\quad153.23458771^\circ$$ $$\beta=\quad2.6691306336\text{ rad},\quad2.4955316306\text{ rad} \\ \quad=\quad152.92992028^\circ,\quad142.98343007^\circ$$ $$\Omega=\quad4.5096853715\text{ sr},\quad3.5896295510\text{ sr} \\ \quad=\quad258.38593872^\circ,\quad205.67062329^\circ$$