3

The Galois theory proof of the improssiblity of angle trisection rests on studying the triple angle formula $\cos 3\theta = 4 \cos^3 \theta - 3 \cos \theta$. Ruler and compass numbers can only be made by adjoining successive quadratic extensions, and we have to adjoin the root of $4x^3 - 3x - \alpha = 0$

In Origami we can trisect the angle and I am trying to understand the proof, here reduce to 4 figures. (pdf from MIT's 6.885)

I found myself challenged by computing the fold described here.

In order to reproduce these figures on my own computer, what is the shape of the grey right triangle in Figure 3? (Still needs and angle $\phi$).

Even more generally, is a question about about the fold in figure $2$. Given

  • line segment $\overline{AB}$ and two lines, $\ell_1, \ell_2$.

How to compute the fold with so that $A' \in \ell_1$ and $B' \in \ell_2$. In the Huzita Axioms of Origami #6.

cactus314
  • 25,084

1 Answers1

0

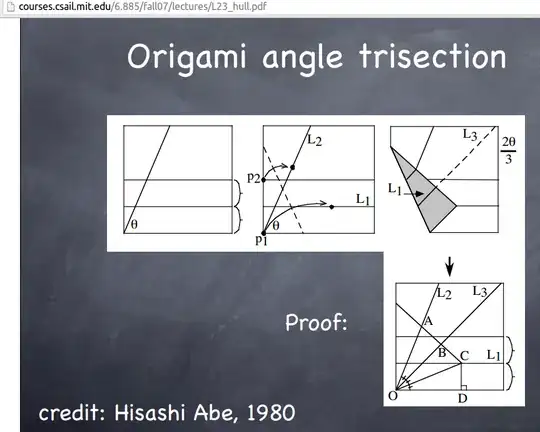
I'll only go up to describing the fold. Let the paper be a unit square. Let $L_1$ be a horizontal line at height $h$, $$ L_1: y=h $$ Then $P_2$ is $(0,2h)$. We name our fold $F_1$, with the ends on $(a,0)$ at the bottom side and $(0,b)$ on the left side (let's assume $a,b > 0$ for now). $$ F_1: y=b-{b\over a}x $$ As we fold, the point $P_1$ on origin $(0,0)$ will be reflected onto point $P'_1$. As it is a reflection, the line connecting $P_1$ and $P'_1$ should be perpendicular to the fold, and the midpoint should lie on the fold. This line is $$ y = {a\over b}x $$ We require $P'_1$ to lie on $L_1$, thus $$ h={a\over b}x $$ therefore $P'_1=({b\over a}h, h)$. Plugging in the midpoint $({b\over 2a}h,{1\over 2}h)$ into $F_1$, we get our first constraint $$ {1\over 2}h=b-{b\over a}\left({b\over 2a} h\right) \\ \therefore a = b\sqrt{h \over h-2b} $$ Let's plug this into $F_1$ $$ F_1: y=b-\sqrt{h-2b\over h}x $$ Next, we have line $L_2$ with a slope $k=\tan \theta$ $$ L_2: y=kx $$ We apply the same argument for reflecting $P_2$ onto $P'_2$. It should lie on the line perpendicular to the fold and passing $P_2$ $$ y=2h+{a\over b}x=2h+\sqrt{h\over h-2b}x $$ while at the same time also lying on $L_2$, thus $$ kx = 2h+{a\over b}x=2h+\sqrt{h\over h-2b}x \\ \therefore P'_2 = \left({2h \over k - \sqrt{h\over h-2b}},{2kh \over k - \sqrt{h\over h-2b}}\right) $$ Then, the midpoint $$ \left({h \over k - \sqrt{h\over h-2b}},h\left(1+{k \over k - \sqrt{h\over h-2b}}\right)\right) $$ should lie on $F_1$ $$ h\left(1+{k \over k - \sqrt{h\over h-2b}}\right) = b - \sqrt{h-2b\over h}\left({h \over k - \sqrt{h\over h-2b}}\right) $$ This determines the value of $b$. Good luck with finding $b$!

When I first saw the intriguing claim that the origami axiom can be used to solve cubic equations, I was filled with excitement. Maybe once and for all I could finally do away with Cardano's or Viete's formulas and have an elegant way of solving. Alas, it is at this very last equation above that I realise that the theorem only looks nice on paper. Finding the fold itself requires you to solve a cubic equation, bringing you back to square one.

syockit
  • 899