Assume, that we have points $x_i$ with $i=1,...,N+1$. We construct the Lagrange basis polynomials as \begin{align} L_j(x) = \prod_{k\not = j} \frac{x-x_k}{x_j-x_k} \end{align}
Now according to my computation and the results by Yves Daoust here, the derivative of $L_i$ can be computed as \begin{align} L'_j(x) = L_j(x)\cdot \sum_{k\not = j}\frac{1}{x_k-x_j} \end{align}
I try to reproduce the numerical results of a paper, and for this results the authors use the derivative matrix $D$ with $D_{ij} =L_i'(x_j)$.
The authors use the Legendre Gauss Lobatto quadrature points, plotted below.
Now I can easily construct the basis polynomials, also plotted below, together with the quadrature points.
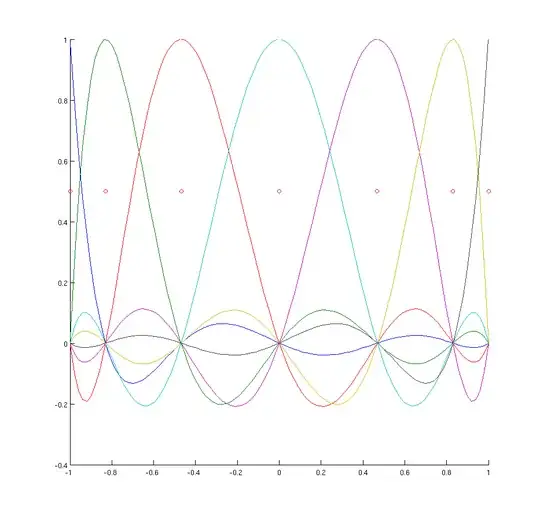
Given the concrete choice of basis points, the plots suggest, that $L'_j(x_j)=0$ except for the first and last basis function. Additionally it seems, that $L'_j(x_i)\not =0$ for $i\not = j$. But using the derived formula from above, we obtain \begin{align} L'_j(x_i) = L_j(x_i)\cdot \sum_{k\not = j}\frac{1}{x_k-x_j}=0 \end{align} for $i\not = j$ since $L_j(x_i) =\delta_{ij}$, which contradicts my observation.
I used the following Matlab functions, to construct the matrix $D$.
function y=dl(i,x,z)
n = length(x);
y = 0;
for m=1:n
if not(m==i)
y = y + 1/(x(m)-x(i));
end
end
size(y)
y = y*l(i,x,z);
end
function y=l(i,x,z)
n = length(x);
% computes h_i(z)
y = 1;
for m=1:n
if not(m==i)
y = y.*(z-x(m))./(x(i)-x(m));
end
end
end
Where dland lare $L'$ and $L$. $D$ is then constructed by
D = zeros(M+1,M+1);
for i=1:M+1
for j=1:M+1
D(i,j) =dl(i,X,X(j));
end
end
which gives the matrix
D =
10.5000 0 0 0 0 0 0
0 -0.0000 0 0 0 0 0
0 0 0.0000 0 0 0 0
0 0 0 -0.0000 0 0 0
0 0 0 0 0.0000 0 0
0 0 0 0 0 0.0000 0
0 0 0 0 0 0 -10.5000
Here I agree with the zeros on the diagonal except for the first and last element. The zeros everywhere else agree with the formula, but they don't agree with my observation.
If I use finite differences (which is no solution for the real implementation) in the following way: FD(i,j) =(l(i,X,X(j)+eps)-l(i,X,X(j)-eps))/(2*eps);
I obtain the output
FD =
-10.5000 -2.4429 0.6253 -0.3125 0.2261 -0.2266 0.5000
14.2016 0.0000 -2.2158 0.9075 -0.6164 0.6022 -1.3174
-5.6690 3.4558 0.0000 -2.0070 1.0664 -0.9613 2.0500
3.2000 -1.5986 2.2667 0 -2.2667 1.5986 -3.2000
-2.0500 0.9613 -1.0664 2.0070 -0.0000 -3.4558 5.6690
1.3174 -0.6022 0.6164 -0.9075 2.2158 -0.0000 -14.2016
-0.5000 0.2266 -0.2261 0.3125 -0.6253 2.4429 10.5000
which is zero on the diagonal (except first and last) and nonzero everywhere else.
So here are my questions:
Did I make an error in the implementation?
Is my formula derived under the assumption that $x$ is not a basis point?
Can I modify my code to obtain the results that my finite difference code produces?
Is my assumption correct, that rather the results of the finite difference computation are "correct"?
EDIT
It seems, like the derivation of the formula goes wrong for $x=x_i$. If I compute the derivative without simplification, I get \begin{align} L_j'(x) = \sum_{l\not = j} \frac{1}{x_j-x_l}\prod_{m\not = (j,l)} \frac{x-x_m}{x_j-x_m} \end{align} Or in code
function y = alternative_dl(j,x,z)
y = 0;
n = length(x);
for l=1:n
if not(l==j)
k = 1/(x(j)-x(l));
for m=1:n
if not(m==j) && not(m==l)
k = k*(z-x(m))/(x(j)-x(m));
end
end
y = y + k;
end
end
end
Which agrees with the finite difference computation.
So it seems to me, that simplifying the above formula includes some "hidden division by zero" if $x=x_i$.
