Scaling and rotating a square so that it is inscribed in the original square

Question

I have a square with a side length of 100 cm. I then want to rotate a square clockwise by ten degrees so that it is scaled and contained inside the existing square.

The image below is what I'm attempting, but with a square, not a triangle. (Image created by Alain Matthes).

And here is the square I'm trying to create, so hopefully this helps:

So my question, how do I determine the distance between the original point and the rotated point? Or, how do I determine the location of the rotated point on its own, independent of the original square? I'm not sure what formula I would use in either instance.

Any assistance in this endeavor would be greatly appreciated.

Answer 1

A more general approach is given as follows. Suppose we have the points $$\zeta_{n,0}^k = \left( \cos \frac{2\pi k}{n}, \sin \frac{2\pi k}{n} \right), \quad k = 0, 1, 2, \ldots, n-1$$ forming a regular $n$-gon with unit circumradius in the Cartesian coordinate plane. We seek a linear transformation $T$ that maps $\zeta_{n,0}^k$ to a point $\zeta_{n,1}^k$ that satisfies the following properties: $$\begin{align*} \zeta_{n,1}^k &= T(\zeta_{n,0}^k) = (1-\lambda) \zeta_{n,0}^k + \lambda \zeta_{n,0}^{\overline{k+1}}, \\ T(0,0) &= (0,0), \end{align*}$$ for each such $k$, where $\overline{k+1}$ is the remainder of $k+1$ divided by $n$. Here, $\lambda \in (0,1)$ is a fixed constant. This suggests a rotation by some angle $\theta$ and scaling by $s$ will work: i.e., $$T(x,y) = \begin{bmatrix}s \cos \theta & -s \sin \theta \\ s \sin \theta & s \cos \theta \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}$$ or if we want to use complex numbers as suggested by our choice of $\zeta$, $$T(z) = se^{i\theta}\zeta_{n,0}^k = se^{i\theta}e^{2\pi i k/n} = se^{i(2\pi k/n + \theta)} = (1-\lambda)e^{2\pi i k/n} + \lambda e^{2\pi i (k+1)/n}.$$ Equivalently, $$se^{i\theta} = 1 + \lambda(\zeta_{n,0} - 1).$$ Solving for $s$ and $\theta$ in terms of $\lambda$, we obtain $$s = \sqrt{\Bigl(1 - \lambda + \lambda \cos \frac{2\pi}{n}\Bigr)^2 + \lambda^2 \sin^2 \frac{2\pi}{n}} = \sqrt{1 - 2\lambda + 2\lambda^2 + 2\lambda(1-\lambda) \cos \frac{2\pi}{n}},$$ $$\theta = \tan^{-1} \frac{\sin \frac{2\pi}{n}}{\frac{1}{\lambda} - 1 + \cos \frac{2\pi}{n}}.$$ The resulting rotation matrix then has the form $$T = \begin{bmatrix} 1 - \lambda + \lambda \cos \frac{2\pi}{n} & -\lambda \sin \frac{2\pi}{n} \\ \lambda \sin \frac{2\pi}{n} & 1 - \lambda + \lambda \cos \frac{2\pi}{n} \end{bmatrix}.$$ Subsequent iterations of $T$ will produce nested $n$-gons with vertices $$T^m(\zeta_{n,0}^k) = \zeta_{n,m}^k.$$

Below is a rather primitive implementation of the above in Mathematica, for $n = 7$ and gradually incrementing $\lambda \in [0.05, 0.95]$:

Answer 2

Let's say your original 4 points are, going counterclockwise from the origin, $$(0,0),(100,0),(100,100),(0,100)$$

You want to rotate clockwise, which means the point that was on the origin will go up to $(0,a)$ and the point that was at $(0,100)$ will go to $(a,100)$. And if you draw out this new situation with all 4 little wedges filling in the space between your new square and the old, you can make triangles with a small leg of $a$ and a long leg of $b$ and you see that $a+b=100$.

So you have a system of two equations and two unknowns. $$a+b=100\\tan(10^{\circ})=\frac{a}{b}$$

This gives $a\approx14.99$. Your new 4 points will be $$(0,14.99),(85.01,0),(100,85.01),(14.99,100)$$

Additionally, each side length was scaled by $0.8632$

EDIT: How to solve the system without a calculator solve() function.

1. Find a numerical value of $tan(10^{\circ})$. It is $0.1763$
2. Solve the first equation in terms of $a$ so $a=100-b$
3. Solve $0.1763=(100-b)/b$ or $0.1763b=100-b\\1.1763b=100\\b=100/1.1763\\b=85.01$

Answer 3

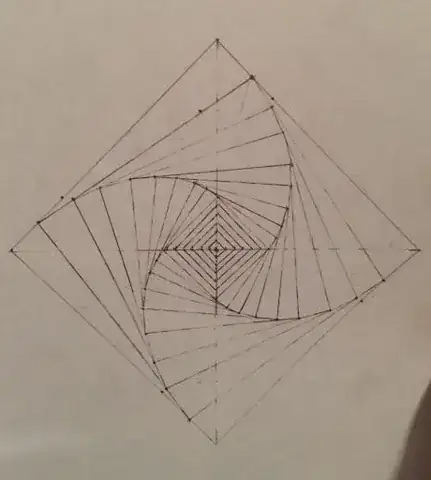
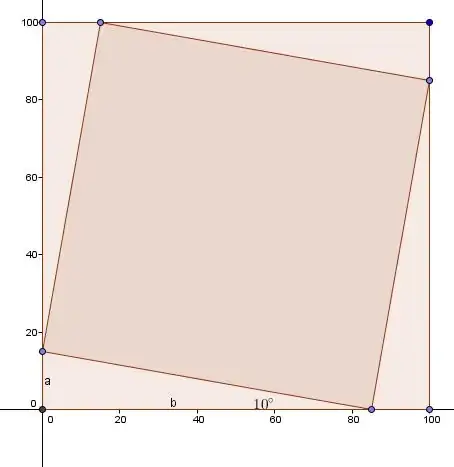
You have two correct answers already. What I would like to do is to put the solution in terms that you can very easily apply to your problem, that is, I want to give you a simple formula to directly compute the coordinates of each vertex of each square.

Let's take polar coordinates with the origin at the center of the square, so that the large square in your diagram has vertices at $(r_0,0)$, $\left(r_0,\frac\pi2\right)$, $(r_0,\pi)$, $\left(r_0,-\frac\pi2\right)$ where $r_0$ is a positive constant determined by how large you want that square to be.

Now we rotate $\delta$ radians to the right and shrink the square so that the new square's vertices lie on the old square's edges. (For a $10^\circ$ rotation, you want $\delta = \frac{\pi}{180} \cdot 10.$) Then the origin, one vertex of the original square, and the corresponding vertex of the new square make a triangle with angle $\delta$ at the origin, $\frac\pi4$ ($45^\circ$) at the original square's vertex, and $\frac{3\pi}{4}-\delta$ at the new square's vertex. Let $r_1$ be the distance from the origin to the new square's vertex. By the law of sines, $$ \frac{r_1}{\sin \left(\frac{\pi}{4}\right)} = \frac{r_0}{\sin \left(\frac{3\pi}{4}-\delta\right)}.$$ Therefore $$r_1 = \frac{\sin \left(\frac{\pi}{4}\right)}{\sin \left(\frac{3\pi}{4}-\delta\right)} r_0 = \frac{\sin \left(\frac{\pi}{4}\right)}{\sin \left(\frac{\pi}{4}+\delta\right)} r_0.$$ Let $$\rho = \frac{\sin \left(\frac{\pi}{4}\right)}{\sin \left(\frac{\pi}{4}+\delta\right)}$$ so that $r_1 = \rho\, r_0.$ For an angle of $10^\circ,$ a little computation shows that $\rho \approx 0.86321799\,$ that is, $$r_1 \approx 0.86321799\, r_0.$$ Checking this against the calculations by @turkeyhundt for the $10$-degree rotation, we should find that $0.86321799 \approx \frac{\sqrt{a^2+b^2}}{100},$ and indeed for $b = 85.01,$ $a=100-b$ that is what we find.

Now observe that in general, if $r_n$ is the distance from the origin to a vertex of the $n$th square, then $r_{n+1} = \rho\, r_n.$ Also, if $\alpha$ is the direction from the origin to a vertex of the $n$th square, then the direction from the origin to a vertex of the $n+1$st square is $\alpha-\delta$ (because polar coordinates measure angles counterclockwise and we are rotating clockwise). Putting these facts together, the vertices of the $n$th square have polar coordinates $$ (\rho^n r_0,\; -n\delta),\\ \left(\rho^n r_0,\; \frac\pi2-n\delta\right)\!,\\ (\rho^n r_0,\; \pi-n\delta),\\ \left(\rho^n r_0,\; -\frac\pi2-n\delta\right)\!. $$ To plot these in Cartesian coordinates, convert the $(r,\theta)$ coordinates of each vertex of each square to $(x,y)$ coordinate by the usual transformation, $x=r\cos\theta$ and $y=r\sin\theta.$ For example, one vertex of the $n$th square will have Cartesian coordinates $(\rho^n r_0 \cos(-n\delta), \rho^n r_0 \sin(-n\delta)),$ and for the other three you simply add a multiple of $\frac\pi2$ to the angle.