14

I don't understand the difference between the dot product of two vectors and the scalar projection of a vector onto another one.

To me it looks like they are both (geometrically) the length of the vector projection. I am wrong since their formulas are different, so can anyone explain why?

John Trentnor
  • 143
  • 1
  • 1
  • 4
  • What do you mean by "the scalar projection"? Evidently, you don't use that phrase to mean the same thing as "the vector projection", so what do you mean by that term? – Gerry Myerson Dec 12 '14 at 05:16
  • 1
    @GerryMyerson: I apologize if this is not a universal term. In my grade 12 class, we defined the scalar projection as $\operatorname{comp}_{\vec{a}}\vec{b}:=\dfrac{\vec{a}\cdot \vec{b}}{||\vec{a}||}$ – John Trentnor Dec 12 '14 at 05:27
  • 1
    We also learned that the vector projection is $\operatorname{proj}{\vec{a}}\vec{b}:=\operatorname{comp}{\vec{a}}\vec{b}\cdot \dfrac{\vec{a}}{||\vec{a}||}$. That is, the vector projection is the scalar projection multiplied by a unit vector in the direction of $a$. – John Trentnor Dec 12 '14 at 05:30
  • Then the dot product doesn't give the length of the vector projection, since the former is $a\cdot b$ while the latter is $a\cdot b/|a|$. I don't see what there is to explain. – Gerry Myerson Dec 12 '14 at 05:34
  • Yeah, I noticed that they have to be different since the formulas are different, but when we did an example with work= $F\cdot D=|F||D|\cos\theta$, our teacher drew the geometric interpretation on the board. He just drew a line from the top vector onto the bottom vector (which was perpendicular to the bottom vector), i.e, a scalar projection. I noticed that scalar projection is would equal the dot product if $||a||=1$, so maybe it has something do with the vector I'm projecting onto having to be a unit vector... – John Trentnor Dec 12 '14 at 05:38
  • 1
    Well, yes, the two formulas are identical if $|a|=1$. – Gerry Myerson Dec 12 '14 at 05:41
  • @GerryMyerson Ah, ok. I must have not noticed that my teacher must have been projecting onto a unit vector. Thanks for the clarification! – John Trentnor Dec 12 '14 at 05:44
  • @JohnTrentnor, indeed, the dot product only gives you the length of the projected vector when the vector being projected onto is of unit length. Otherwise, you'll get its length scaled by the length of that other vector. – Severyn Kozak Sep 20 '15 at 18:05

3 Answers3

23

Projection

The component of a vector a that is in the same direction as of vector b (Hence projection is a vector) Length of the projection does not depend on the length(magnitude) of b. See the image below

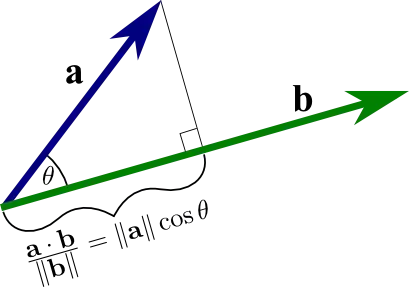
enter image description here

Projection has two parts:

(i) The direction where you're projecting onto. That's the unit vector in direction of b, which is computed by dividing b by the length of b. That is $$\frac{b}{||b||}$$

(ii) The component of a in the direction of b. That is, the "shadow" or image of a when you project it onto b. This is computed by $$\frac{a⋅b}{||b||}$$ . because a⋅b=||a|| ||b|| cos(θ). Hence

||a||cos(θ)= $\frac{a⋅b}{||b||}$
and that gives you (as in the triangle figure), the length of a's projection on the direction of b

Putting it together, the projection of a onto b is a vector of length $$\frac{a⋅b}{||b||}$$

in the direction of $\frac{b}{||b||}$, i.e. $$\frac{a.b}{||b||} \frac{b}{||b||} $$

Dot Product

It's simply the projection of one vector onto the other multiplied by the magnitude of other vector. The dot product tells you what amount of one vector goes in the direction of another (Thus its a scalar ) and hence do not have any direction .

a.b= ||a|| ||b|| cos(θ). Alternatively if a=(x1,y1) and b=(x2,y2) (Position vectors) the dot product is x1.x2+y1.y2 .

Vijay P R
  • 331
1

The output of a dot product is a real number. The output of a projection is a vector. If you look at the formulas, the scalar projection does not depend on the length of the vector you are projecting onto.

According to Wikipeda, the scalar projection does not depend on the length of the vector being projected on. If you double the length of the second vector in the dot product, the dot product doubles.

Ross Millikan
  • 383,099
  • 1
    It seems to me from the wording of the question that OP is making some distinction between "scalar projection" and "vector projection", though I'm not sure what exactly the first one is supposed to be. – Gerry Myerson Dec 12 '14 at 05:17
  • 1
    @GerryMyerson: I found a Wikipedia page on scalar projection It is a vector in the direction of the second argument with the magnitude of the dot product between the first argument and the unit vector in the direction of the second argument. I have no clue why this would be of interest. – Ross Millikan Dec 12 '14 at 05:21
  • Thanks. OP has just provided the definition his class is using, and it's a scalar, not a vector. – Gerry Myerson Dec 12 '14 at 05:30
0

As described above in comments, dot product and scalar projection are same when projecting onto a unit vector.

When we're projecting a vector b on a non-unit vector, here a, then scalar projection finds respective unit vector (normalize a by dividing by norm ||a||) and projects on the unit vector. However, dot product doesn't do this normalization.

Dot product is simply ||a|| * projection of b (onto a) $$ =\||a\|| * \frac{a.b}{||a||} = a.b$$

Anjali
  • 1