2

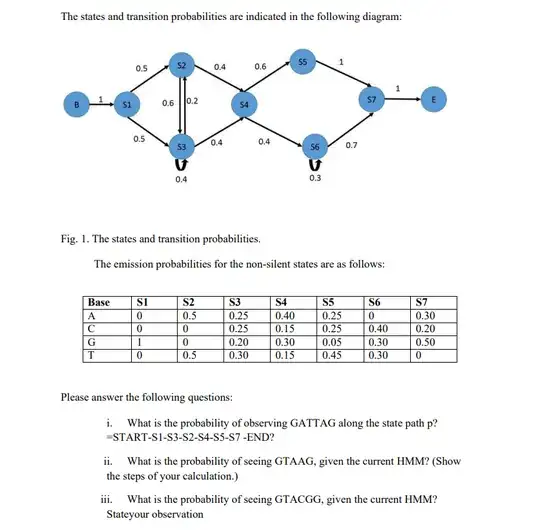
I am trying to find answers to the following questions. Can someone please help. This is a Hidden Markov Model with 7 states and 4 observations. I have worked out the following solution but still need help with parts ii & iii.

enter image description here

Solution:

I. GATTAG = 1* 1 * 0.5 * 0.25 * 0.2 * 0.5 * 0.4 * 0.15 * 0.6 * 0.25 * 1 * 0.5 * 1 =0.00005625

II. GTAAG

possible paths: B -> S1-> S2 -> S4 -> S5 -> S7-> E

=>1 * 1 * 0.5 * 0.5 * 0.4 * 0.4 * 0.6 * 0.25 * 1 * 0.5 * 1 =

B -> S1-> S2 -> S4 -> S6 -> S7-> E

=> 1* 1 * 0.5 * 0.5 * 0.4 * 04 * 0.4 * 0 * 0.7 * 0.5 * 1 = 0

B -> S1-> S3-> S4 -> S6 -> S7-> E

=> 0

B -> S1-> S3-> S4 -> S5 -> S7-> E

=> 1 * 1 * 0.5 * 0.3 * 0.4 * 0.4 * 0.6 * 0.25 * 1 * 0.5 * 1 =

III. GTACGG

possible paths: B -> S1-> S2-> S3-> S4 -> S6 -> S7-> E

B -> S1-> S2-> S3-> S4 -> S5 -> S7-> E

B -> S1-> S3 -> S2-> S4 -> S6 -> S7-> E

B -> S1-> S3 -> S2-> S4 -> S5 -> S7-> E

B -> S1-> S3 -> S3-> S4 -> S6 -> S7-> E

B -> S1-> S3 -> S3-> S4 -> S5 -> S7-> E

B -> S1-> S3 -> S4 -> S6 -> S6 -> S7-> E

B -> S1-> S2 -> S4 -> S6 -> S6 -> S7-> E

How do I calculate this probability?

Maninder Preet Singh Puri
  • 33
  • 5

1 Answers1

1

The total probability is simply the sum of all the probabilities from the different paths. In probability terms it's the union of disjoint events, that's why the probabilities can be summed.

Erwan
  • 26,519
  • 3
  • 16
  • 39