Why Mini batch gradient descent is faster than gradient descent?

Question

As I understand them:

Mini Batch Gradient Descent :

1. It takes a specified batch number say 32.
2. Evaluate loss on 32 examples.
3. Update weights.
4. Repeat until every example is complete.
5. Repeat till a specified epoch.

Gradient Descent :

1. Evaluate loss for every example.
2. Update loss accordingly.
3. Repeat till a specified epoch.

My questions are:

1. As Mini batch GD is updating weights more frequently, shouldn't it be slower than normal GD?
2. Also I have read somewhere that we estimate loss in SGD (i.e. we sacrifice some accuracy in loss calculation for speed). What does it mean, and does it help in increasing speed?

Answer 1

1. It is slower in terms of time necessary to compute one full epoch. BUT it is faster in terms of convergence i.e. how many epochs are necessary to finish training which is what you care about at the end of the day. It is because you take many gradient steps to the optimum in one epoch when using batch/stochastic GD while in GD you only take one step per epoch. Why don't we use batch size equal 1 every time then? Because then we can't calculate things in parallel and computation resourses are not used efficiently. It turns out in every problem there is a batch size sweet spot which maximises training speed by balancing how parallelized your data is and number of gradient updates per epoch.
2. mprouveur answer is very good; I'll just add that we deal with this problem by simply calculating average or sum loss over all batches' losses. We don't really sacrifice any accuracy i.e. your model is not worse off because of SGD - it's just that you need to add up results from all batches before you can say anything about the results.

Answer 2

1 - The computation time of SGD is much lower than GD as you only use a subset of the whole data, that is why it is actually faster (time-wise) even though it seems you do more stuff.

2- With GD you compute your gradient on all the data you have, therefore the computed gradient gives you the best direction to minimize your function on the whole dataset. With SGD however, each gradient step only uses a subset of the data, the minimization direction is therefore best for this subset but it does not account for all your data. However as you randomly pick samples of your data, in average you will go in the right direction and the more samples you use, the more accurate (but expensive) your gradient is.

Answer 3

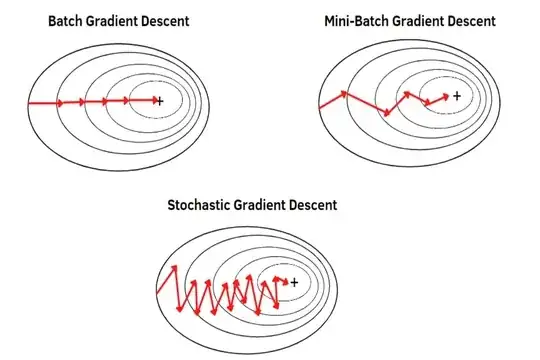
Batch Gradient Descent(BGD) uses the average of a whole dataset, so each sample is not stood out(not emphasized). As a result, the computation is stable(not fluctuated), getting an accurate value but BGD sometimes gets stuck in local minima because the computation is stable(not fluctuated) as I said before.

Mini-Batch Gradient Descent(MBGD) uses the average of each small batch splitted from a whole dataset so each sample is stood out(emphasized). *Splitting a whole dataset into smaller batches can make each sample more stood out(more emphasized). As a result, the computation is less stable(more fluctuated) than BGD, getting a less accurate value than BGD but MBGD less gets stuck in local minima than BGD because the computation is less stable(more fluctuated) than BGD as I said before.

Stochastic Gradient Descent(SGD) uses every single sample of a whole dataset one sample by one sample but not the average so each sample is more stood out(more emphasized) than MBGD. As a result, the computation is less stable(more fluctuated) than MBGD, getting a less accurate value than MBGD but SGD less gets stuck in local minima than MBGD because the computation is less stable(more fluctuated) than MBGD as I said before.

_{This image is from statusneo.com.}