Feature scaling worsens performance?

Question

I noticed that feature scaling can destroy completely neural networks performance in some cases. Below are my results that you can reproduce easily.

I use a neural network to approximate function $g$ on $[0,100]$ as follows:

$\mathcal{N}\mathcal{N}(X; \theta) \approx g(X)$

where $X \sim \mathcal{U}([0,100])$. Then I randomly sample some $X$ ($(X_i)_i$) to be my training set, and use $Y_i=g(X_i)$ as targets.

Typically $\mathcal{N}\mathcal{N}$ is a Keras Sequential model, and has a few hidden layers with 15-20 neurons (elu), and a single output layer with no activation function. Parameters are initialized using kernel_initializer='normal'.

Now I noticed the following while testing my approximations in 1dim (before trying to generalize to higher dimensions):

For $g(x)=\max(0, X-50)$, scaling $X$ by dividing it by 100 does not really change the performance of the $\mathcal{N}\mathcal{N}$, which estimates $g$ relatively well.

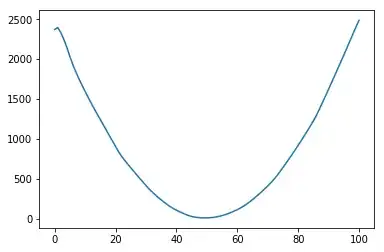
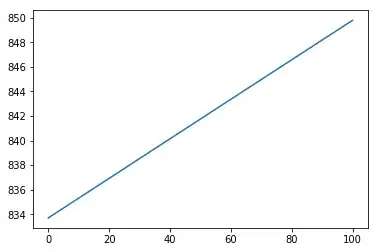
However, when I use other functions such as $g(x)=1-\mathbb{I}_{x\in[40,60]}$ or $g(x)=(x-50)^2$, it fails completely.

Do you have an explanation?

This is very disturbing because how can you trust your network to approximate high-dimensional functions if it fails completely for simple 1-dimensional examples?

Below is an example implementation in Python:

from keras.models import Sequential
from keras.layers import Dense
import numpy as np
import matplotlib.pyplot as plt

d=1
nn_value_batch_size=128
nn_value_epochs=50
nn_value_training_size=10000

def nn_value_get_architecture(layers_sizes):
        nn_value = Sequential()
        nn_value.add(Dense(layers_sizes[0], input_dim=d, #d=1
                        kernel_initializer='normal', activation='elu'))

        # hidden layers
        for nb in layers_sizes[1:]:
            nn_value.add(Dense(nb, kernel_initializer='normal',
                               activation='elu'))

        # output layer
        nn_value.add(Dense(1, kernel_initializer='normal'))

        nn_value.compile(loss="mean_squared_error", optimizer='adam')
        return nn_value

def nn_value_optimize(nn_value, objective_function,
                          x_normalize=True):
        # fit the model
        x_distribution = lambda size: np.random.uniform(0, 100, size)
        for epoch in range(nn_value_epochs):
            X_train = x_distribution(nn_value_training_size)
            y_train = objective_function(X_train)
            if x_normalize==True:
                X_train = X_train/100
            nn_value.fit(X_train, y_train,
                         batch_size=nn_value_batch_size,
                         verbose=1)

        return nn_value

def g(X):
        #return 1-(np.maximum(0., X-40)/(X-40) - np.maximum(0., X-60)/(X-60))
        return (X-50)**2
        #return np.maximum(0., X-50) #only example that works

nn_value = nn_value_get_architecture(
                layers_sizes=[20,15,15,15,15])
g = np.vectorize(g)
normalize=True
nn_value = nn_value_optimize(nn_value, g, normalize)

# plot results
x = np.arange(0,101,1)
if normalize==True:
  plt.plot(x, nn_value.predict(x/100))
else:
  plt.plot(x, nn_value.predict(x))
plt.show()

No scaling:

With scaling:

Answer 1

By scaling X but not y, and having small weights at initialization, I think you are making it hard for the NN to bring the weights up to the scale they need to be. Possibly if you let it train for more epochs it would find the right scale, but quick experimentation suggests it gets stuck into an oscillating loss that is quite large.

I had success in reaching a parabolic curve by either (1) scaling y as well, to land roughly in $[0,1]$, or (2) setting the initial weights to be larger, e.g. from keras import initializers; nn_initializer=initializers.RandomNormal(std=0.5) and using kernel_initializer=nn_initializer throughout. (The default for std in RandomNormal is 0.05).

For the indicator function target, obviously scaling y isn't the issue. But interestingly, scaling up the initial weights does work. Maybe because you need to get those two large-slope bits at 40 and 60?

One other thing I'd suggest trying (I haven't here) is varying the learning rate, dependent on the scale of things. Especially when the initial weights are far below what we know they'll need to end up as, maybe a large initial learning rate with some decay would help.