I am working on a highly-imbalanced binary-labeled dataset, where number of true labels is just 7% from the whole dataset. But some combination of features could yield higher than average number of ones in a subset.
E.g. we have the following dataset with a single feature (color):
180 red samples — 0
20 red samples — 1
300 green samples — 0
100 green samples — 1
We can build a simple decision tree:
(color)
red / \ green
P(1 | red) = 0.1 P(1 | green) = 0.25
P(1) = 0.2 for the overall dataset
If I run XGBoost on this dataset it can predict probabilities no larger that 0.25. Which means, that if I make a decision at 0.5 threshold:
- 0 - P < 0.5
- 1 - P >= 0.5
Then I will always get all samples labeled as zeroes. Hope that I clearly described the problem.
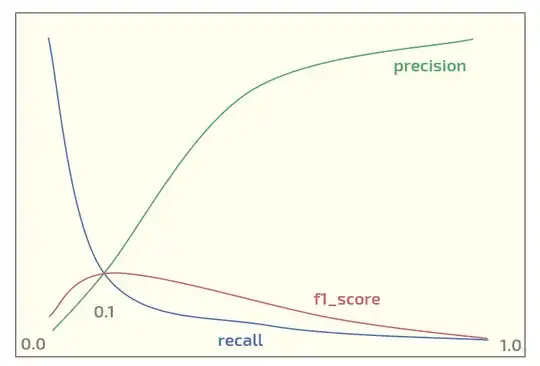
Now, on the initial dataset I am getting the following plot (threshold at x-axis):
Having maximum of f1_score at threshold = 0.1. Now I have two questions:
- should I even use f1_score for a dataset of such a structure?
- is it always reasonable to use 0.5 threshold for mapping probabilities to labels when using XGBoost for binary classification?
Update. I see that topic draws some interest. Below is the Python code to reproduce red/green experiment using XGBoost. It actually outputs the expected probabilities:
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
import numpy as np
X0_0 = np.zeros(180) # red - 0
Y0_0 = np.zeros(180)
X0_1 = np.zeros(20) # red - 1
Y0_1 = np.ones(20)
X1_0 = np.ones(300) # green - 0
Y1_0 = np.zeros(300)
X1_1 = np.ones(100) # green - 1
Y1_1 = np.ones(100)
X = np.concatenate((X0_0, X0_1, X1_0, Y1_1))
Y = np.concatenate((Y0_0, Y0_1, Y1_0, Y1_1))
# reshaping into 2-dim array
X = X.reshape(-1, 1)
import xgboost as xgb
xgb_dmat = xgb.DMatrix(X_train, label=y_train)
param = {'max_depth': 1,
'eta': 0.01,
'objective': 'binary:logistic',
'eval_metric': 'error',
'nthread': 4}
model = xgb.train(param, xg_mat, 400)
X0_sample = np.array([[0]])
X1_sample = np.array([[1]])
print('P(1 | red), predicted: ' + str(model.predict(xgb.DMatrix(X0_sample))))
print('P(1 | green), predicted: ' + str(model.predict(xgb.DMatrix(X1_sample))))
Output:
P(1 | red), predicted: [ 0.1073855]
P(1 | green), predicted: [ 0.24398108]