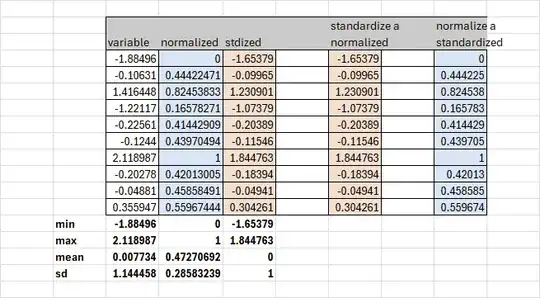
When I combine standardizing and normalizing my input data for my hybrid ANN model, it gives the best results.
But I can't find anywhere, why. I based it on a paper's approach but they don't justify their practice either. Anyone knows why?
Standardization of my input data gives R2 less than 0.71, a higher RMSE and less stable results, than both standardizing and normalizing my input data.
Random initialization: initial_weights = np.random.randn((inputs * hiddens) + (hiddens * outputs)) Xavier initialization: limit = np.sqrt(6 / (n_in + n_out)) For stand with random initialization, RMSE: 43.9268, R^2: 0.4678 For stand with xavier initialization, RMSE: 36.7307, R^2: 0.6279 For stand-norm with random initialization, RMSE: 32.0556, R^2: 0.7166. My model converges quicker, better and more stable with stand-norm with random initialization. R^2 used is coefficient of determination.