Welcome to DS.SE @h_ihkam !
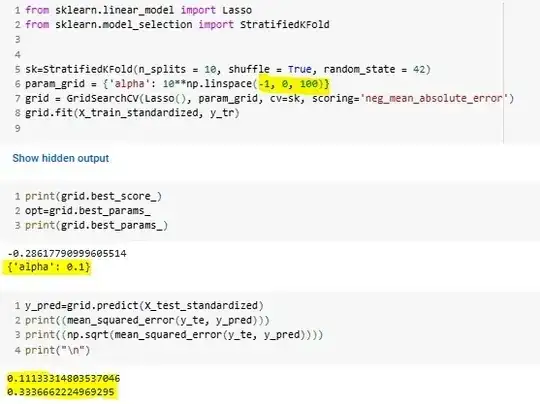
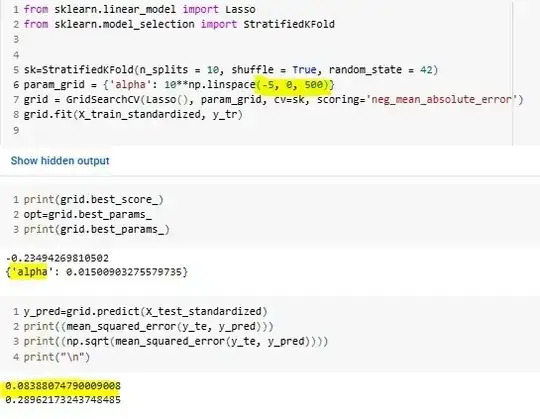
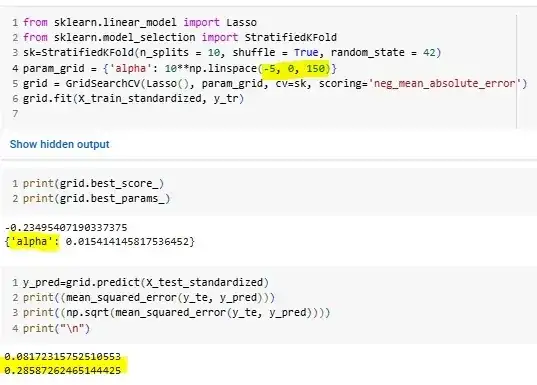
So how can I decide on the search range? What is the best practice? Please provide me with some guidance.
Good questions !!
Choosing the Optimal Lambda in LASSO Using Cross-Validation
The objective of cross-validation in LASSO regression is to select the optimal regularisation parameter $\lambda$, which determines the extent of penalisation on the regression coefficients. This helps to ensure that a balance between model complexity and predictive accuracy, helping to prevent overfitting while maintaining interpretability.
1. Understanding LASSO Regression
LASSO regression augments ordinary least squares with an $\ell_1$ penalty, defined as:
$$
\text{Minimise: } \frac{1}{2n} \sum_{i=1}^n (y_i - \mathbf{x}_i^\top \boldsymbol{\beta})^2 + \lambda \sum_{j=1}^p |\beta_j|
$$
Where:
- $n$: Number of observations.
- $p$: Number of predictors.
- $y_i$: Response variable for observation $i$.
- $\mathbf{x}_i$: Predictor vector for observation $i$.
- $\boldsymbol{\beta}$: Vector of regression coefficients.
- $\lambda$: Regularisation parameter controlling the penalty strength.
As $\lambda$ increases, more coefficients shrink to zero, effectively performing variable selection and enhancing model interpretability.
2. Selecting Optimal Lambda with Cross-Validation
a. Generate a Range of Lambda Values
Create a grid of $\lambda$ values, typically on a logarithmic scale (eg., $10^{-4}$ to $10^2$), to explore varying levels of penalisation.
b. Perform $k$-Fold Cross-Validation
- Divide the data into $k$ folds.
- For each $\lambda$, iteratively:
- Fit the LASSO model on $k-1$ folds.
- Compute validation error (eg., mean squared error) on the remaining fold.
c. Aggregate Validation Errors
Compute the mean validation error across the $k$ folds for each $\lambda$, providing a robust estimate of model performance.
d. Choose Optimal Lambda
Select the $\lambda$ minimising the average validation error. Alternatively, use the "1-standard error rule," selecting the simplest model (largest $\lambda$) within one standard error of the minimum error. This approach enhances interpretability by favouring more parsimonious models.
3. Implementation in Python
Example Using sklearn
from sklearn.linear_model import LassoCV
import numpy as np
Generate example data
X = np.random.rand(100, 10) # Features
y = np.random.rand(100) # Target
Perform LASSO with cross-validation
lasso_cv = LassoCV(alphas=np.logspace(-4, 2, 100), cv=5, random_state=42)
lasso_cv.fit(X, y)
Extract optimal lambda and coefficients
optimal_lambda = lasso_cv.alpha_
optimal_coefficients = lasso_cv.coef_
print(f"Optimal Lambda: {optimal_lambda}")
print("Optimal Coefficients:", optimal_coefficients)
4. Key Considerations
a. Standardise Predictors
Predictors must be standardised (mean 0, variance 1) as LASSO is sensitive to variable scales. Without standardisation, coefficients may be penalised disproportionately, leading to suboptimal model selection.
b. Model Validation
Cross-validation provides an unbiased estimate of model performance. However, it is essential to evaluate the final model on an independent test set to confirm its generalisability.
c. Multicollinearity
LASSO is effective at handling multicollinearity by selecting a single variable from a group of highly correlated predictors. This makes it particularly suitable for datasets with collinear features.
d. 1-Standard Error Rule
The 1-standard error rule enhances interpretability by selecting the simplest model (largest $\lambda$) within one standard error of the minimum cross-validation error. This avoids overfitting while maintaining predictive performance.
5. Common Pitfalls
- Insufficient Cross-Validation Folds: Using too few folds (eg., $k = 3$) may produce high variance in performance estimates. It is recommended to use $k = 5$ or $k = 10$ for more reliable results.
- Default Parameter Reliance: Blindly relying on default $\lambda$ ranges may result in suboptimal models. Instead, tailor the range of $\lambda$ values to the dataset’s scale and complexity.
- Ignoring Simplicity: Failing to apply the 1-standard error rule can lead to overly complex models that risk overfitting and reduced interpretability.
6. Further related Topics
Elastic Net
Elastic Net is an extension of LASSO that combines $\ell_1$ and $\ell_2$ regularisation, addressing scenarios where LASSO's variable selection is overly aggressive. Its objective function is:
$$
\text{Minimise: } \frac{1}{2n} \sum_{i=1}^n (y_i - \mathbf{x}_i^\top \boldsymbol{\beta})^2 + \lambda \left( \alpha \sum_{j=1}^p |\beta_j| + \frac{1-\alpha}{2} \sum_{j=1}^p \beta_j^2 \right)
$$
Here:
- $\alpha$: Controls the trade-off between LASSO ($\ell_1$) and Ridge ($\ell_2$) penalties.
- $\lambda$: Overall regularisation parameter.
Elastic Net is especially useful in high-dimensional datasets where groups of correlated variables need to be selected together.
Stability Selection
Stability selection improves the robustness of variable selection by repeatedly resampling data subsets and identifying predictors consistently chosen across models. This is effective for high-dimensional datasets with noisy predictors.
Conclusion
Cross-validation is a very important tool for selecting the regularisation parameter $\lambda$ in LASSO regression. By balancing model complexity and predictive performance, it helps to ensure that models generalise effectively to unseen data. While libraries like sklearn simplify implementation, understanding the principles behind LASSO and related methods like Elastic Net can help avoid common pitfalls and refine the model selection process.
References
- Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B: Statistical Methodology, 58(1), 267-288.
https://www.math.cuhk.edu.hk/~btjin/math6221/p7.pdf
- Meinshausen, N., & Bühlmann, P. (2010). Stability selection. Journal of the Royal Statistical Society Series B: Statistical Methodology, 72(4), 417-473.
https://arxiv.org/pdf/0809.2932