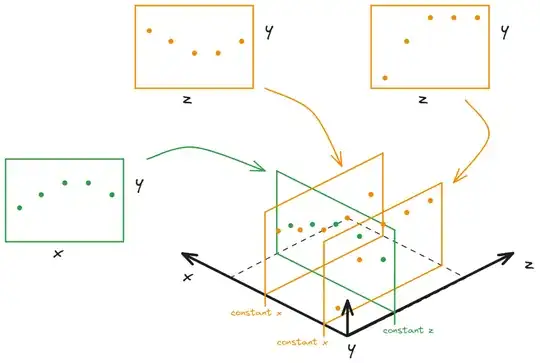
I am having some trouble approaching some data modelling of the following structured dataset I'm trying to analyse, and then creating a surface from it.
So I have 3 variables: say x, y, and z (variable names changed for simplicity), where y is dependent on x and z. x and z are independent variables.
The datasets I have are 1 x-y datasheet at a constant z, and 2 z-y datasheets at constant x values, x1 and x2.
How should I approach modelling the evolution of y with x and z, given that I don't have a continuous relation between x and z?
My attempt was to use the griddata interpolation method by concatenating pairs of (x/z arrays, respective constants) as points, and concatenating the y data together as values. I have rewritten a simplified version of what I'm doing below.
My issue here is that I'm not sure I'm approaching this problem in the right way, as I'm not getting a convincing visualisation. I'm not sure whether I should take a predictor approach, however due to the lack of data (no (X, Y, Z) set), that might not be very possible (unless there's a method I'm not thinking of).
x = x_arr # Independent array 1
z = z_arr # Independent array 2
x1 = 5 # Constant value of x in the z-y data
x2 = 20 # Another constant value of x in the z-y data
z1 = 0 # Constant value of z in the x-y data
y_x1_constant = x1_const_arr # y(z) values at constant x = x1
y_x2_constant = x2_const_arr # y(z) values at constant x = x2
y_z1_constant = x3_const_arr # y(x) values at constant z = z1
points = np.array([ # Concatentating pairs of array, constant
zip(x, [z1]len(x)),
zip([x1]len(z), y),
zip([x2]len(y), y)
])
values = np.concatenate(y_z1_constant, y_x1_constant, y_x2_constant) # Setting the values
interp = griddata(points, values, (xi, yi), method='cubic') # Interoplating using grid data, where (xi, yi) is some meshgrid