About the 'trick' for finding the diameter of an graph in $O(n^2)$

Question

The diameter of an undirected, unweighted graph can be found in $O(n^3)$ with e.g. the Floyd–Warshall algorithm. However, there is an idea how to improve the runtime:

1. Pick a vertex $v$
2. Find $u$ such that $d(v,u)$ is maximum
3. Find $w$ such that $d(u,w)$ is maximum
4. Return $d(u,w)$

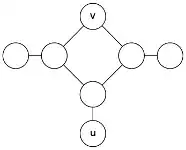
This idea fails; for instance, when starting at $v$ here:

However, it is not immediately clear to me if we can not amend the above algorithm with another indirection, and also consider all nodes with maximum distance instead of only one. That is:

1. Pick a vertex $v$
2. Find the set $U$ such that $u \in U \implies d(v,u)$ is maximum
3. For each node $u$ in $U$, find the set $W_u$ such that $w \in W \implies d(u,w)$ is maximum
4. Merge these sets $W_u$ into a new set $W$
5. Calculate the eccentricity of all nodes in $W$
6. Return the maximum eccentricity found this way

The improved algorithm works for the above counterexample as well as others (e.g. this one).

I assume it is still wrong. If it were not, it would offer a significant improvement for at least some kinds of graphs. Is there a counterexample? And how could a counterexample for further additional indirections be constructed?

Answer 1

The diameter of the following graph is $2a+4$. If you start from $v$, you will need $i=2a+1$ iterations to have $s,t\in W_{i}$. It provides a family of counter-examples for an arbitrary large number of indirections (as $a \to \infty$).