Do exponents have higher time complexity than factorials?

Question

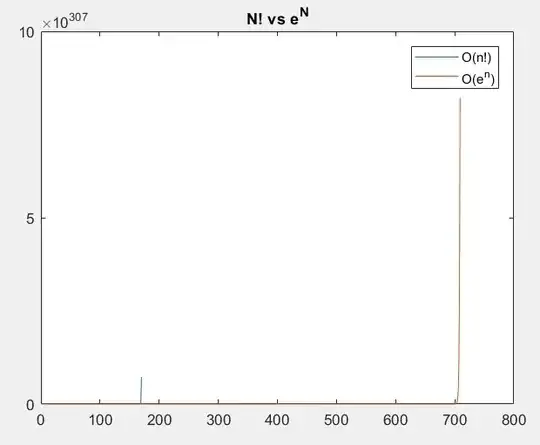
My professor said exponentials will always have higher time complexity compared to polynomials. My question is, do exponentials also have higher time complexity than factorials?

I plotted a chart in Matlab to check it myself.

When range of x is small, from 1 to 10, I get the following chart,

%Matlab script
x  = [1 : 10];
y1 = factorial(x);
y2 = exp(x);

plot(x', [y1',y2']);
title("N! vs e^N");
legend("O(n!)", "O(e^n)");

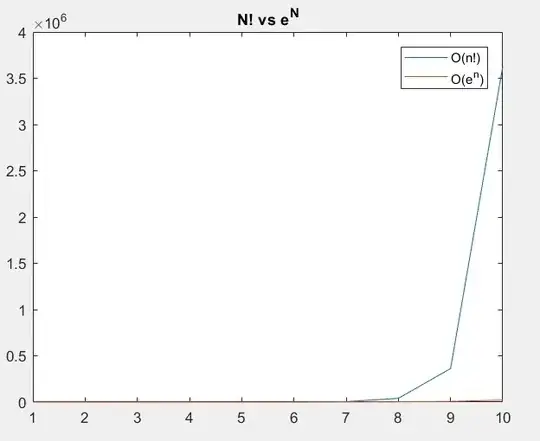Here factorial is clearly beating exponential.

But when I bump the range of x from 1 to 1000, I get the following chart,

x  = [1 : 1000];

Here exponential is clearly beating factorial.

So, can I say conclusively that exponentials will always have higher time complexity than both factorials and polynomials?

-

score 3 · Accepted Answer · edited Jun 16 '20 at 10:30

In fact $e^n$ is $o(n!)$. We could show it using the Stirling approximation by taking limit $$\lim_{n\rightarrow \infty}{\frac{e^n}{(\sqrt{2\pi n})(\frac{n}{e})^n}} = \lim_{n\rightarrow \infty}{\frac{e^{2n}}{(\sqrt{2\pi n})n^n}} = \lim_{n\rightarrow \infty}{\frac{1}{\sqrt{2\pi n}}\frac{e^{2n}}{n^n}}$$

Since $\lim_{n\rightarrow \infty}{\frac{1}{\sqrt{2\pi n}}} = 0$ we only need to calculate $$\lim_{n\rightarrow \infty}{\left(\frac{e^2}{n}\right)^n}$$ The function $\frac{e^2}{n}$ decreases faster than any function $c^n$ where $0 < c < 1$ for sufficiently large $n$s (as $n$ goes to infinity), and so $\lim_{n\rightarrow \infty}{\left(\frac{e^2}{n}\right)^n} = 0$.

Regarding Quazi Irfan's comments about Matlab graph
I am not a Matlab user, but these are plots for $e^x$ and Stirling approximations of $n!$ using Wolfram script: plot (1\sqrt(2*pi*x)*(x/e)^x) from 0 to 6, plot(e^x) from 0 to 6

As you see $n!$ overtakes $e^n$ when $n=6$.

Do exponents have higher time complexity than factorials?

1 Answers1