2

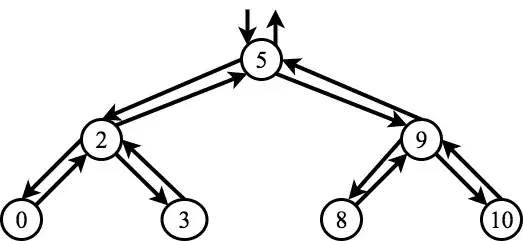
Prove that given a number we can find whether there're 2 elements in a red/black tree that their sum equals that number in $\Theta(n)$ time and constant space.

The original problem appears here, however the solution uses $\lg n$ space. A problem in my course required adjusting the algorithm such that we use constant space.

I thought of the following algorithm:

MyAlgorithm(root, num)
    min<-findMin(root)
    max<-findMax(root)
    while(min.key <= max.key && min != max)
        if((min.key + max.key)=num) return true
        if((min.key + max.key) < num)
            min<-successor(min)
        else
            max<-predeccessor(max)
    return false

According the CLRS book both predeccessor() and successor() functions time complexity depends on tree height which is $O(\lg n)$ in our case since red-black tree is balanced.

However, we have the while loop which theoretically can run almost n times.

For example, because the algorithm above is equivalent to searching for the number num in a sorted array, say we have this array and num<-3: $$ 1,2,3,4,5,6,7,8,9,10 $$ In this case we'll call predecessor(max) $8$ times which is almost $\Theta(n)$ or $\Theta((n-2)\lg n)=\Theta(n\lg n)$ asymptotically.

Am I wrong in my conclusions? How can I prove that the time complexity is indeed $\Theta(n)$?

D.W.
  • 167,959
  • 22
  • 232
  • 500
Yos
  • 527
  • 1
  • 5
  • 18

2 Answers2

2

So we are given a binary search tree $T$ (we, however, do not require it to be balanced). Also we are given an integer; let's call it target_number. We wish to query whether there are two distinct nodes in $T$ such that the sum of their values equals target_number. In order to do that, we need two functions: get_successor(x) and get_predecessor(x). Given a node x get_successor(x) returns the tree node whose value is larger than that of x and is the smallest such value. The definition of get_predecessor(x) is symmetric.

The algorithm is now (as in your question): point to the minimum node, and point to the maximum node. Compute the sum $S$ of the nodes pointed by the two pointers. If $S$ is less than the target number, move left pointer to its successor node. If $S$ is greater than the target number, move right pointer to its predecessor node. Otherwise, we have a match and return true.

query(root, target_number)
    left_finger  = the minimum node of the entire tree rooted at root
    right_finger = the maximum node of the entire tree rooted at root

    while left_finger != nil and right_finger != nil and left_finger != right_finger
        tentative_sum = left_finger.value + right_finger.value
        if tentative_sum < target_number
            left_finger = get_successor(left_finger)
        else if tentative_sum > target_number
            right_finger = get_predecessor(right_finger)
        else
            return true
    return false

Next, we need to give a strong argument that it runs, in fact, in $\Theta(n)$. Take a look at operation get_successor: If you start from the minimum node and visit the entire tree in successor order, you do $\Theta(n)$ work regardless the fact that get_successor runs in worst case $\mathcal{O}(\log n)$, and that is why: you visit each node at most three times: from the parent, returning from the left child and returning from the right child; we spend constant time at each node.

As you can see from the below diagram, each node x has at most 3 incoming arcs and has at most 3 outgoing arcs. Traversing each arc is $\Theta(1)$. So basically, if we start from a minimum node, and keep advancing to the successor nodes, we do essentially in-order traversal that is, however, iterative instead of recursive. Same argument for starting from the maximum node via get_predecessor.

Now, we do the same traversal but in "both directions" (the left_finger proceeds towards successor nodes and right_finger proceeds towards predecessor nodes, and we terminate (at latest) when the two fingers meet. Thus, running time is linear in tree size and space complexity constant since no recursion is involved.

In-order traversal and successor traversal

coderodde
  • 60
  • 1
  • 13
-1

First thing that popped into my mind, was using a hashmap (or just a key - storage) while iterating.

In the HashTable, I would store an addend for the sum, and while iterating I would look up if the value is in the list.

Addends[] //KeySet
for value in Values {
   if(Addends.contains(value) // Pair found
     return true
   Addends.add(Sum - value)
}
scoobycode
  • 101