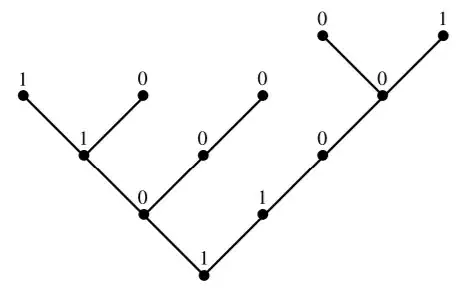
I've started with tree automata. The definition is
(Leaf-to-root) Tree automaton $\mathcal M$ over (nonempty, finite) alphabet $\Sigma$ is quintuple $\mathcal M=(K,\Sigma,\delta,S,F)$ and bound $f$ (the fan-in bound), where $K$ is finite set of states, $S\subseteq K$ set of initial states, $F\subseteq K$set of accepting states with $\delta:A\to K$ for some (nonemty?) $A\subseteq\bigcup\limits_{i=1}^f\underbrace{K\times\cdots\times K}_i\times\Sigma$.
It seems ok to me, but when it comes to an example I'm lost. For example consider following tree automaton over $\{0,1\}$
I suppose $S$ is set of leaves. And now what is example of word $w$ accepted by the automaton? And how is the word read by it?
Thx a lot for help...