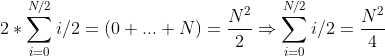Why is the time complexity of insertion sort not brought down even if we use binary search for the comparisons?

Question

There are two factors that decide the running time of the insertion sort algorithm:
the number of comparisons, and the number of movements.
In the case of number of comparisons, the sorted part (left side of $j$) of the array is searched linearly for the right place of the $j^{th}$ element. If instead, we use a binary search, then the time complexity of finding a place for the $j^{th}$ element comes down from $\operatorname{O}(n)$ to $\operatorname{O}(\log n)$. So, for all the $n$ elements, the time complexity for comparisons becomes $\operatorname{O}(n \log n)$. Even so, the number of movements is still going to take $\operatorname{O}(n)$ time, and the total time complexity isn't brought down and remains $\operatorname{O}(n^2)$. Why is that?

Are any of my statements wrong assumptions?

Can a possible explanation be: the total time complexity isn't brought down and remains $\operatorname{O}(n^2)$. This is because to search an element (using binary search) it takes $\operatorname{O}(\log n)$ time, and to move the elements it takes $\operatorname{O}(n)$ time. Total cost is $\operatorname{O}(\log n)+\operatorname{O}(n)=\operatorname{O}(n)$ time. To do this for $n-1$ elements, it takes $n(n-1)=\operatorname{O}(n^2)$ time?

Answer 1

For the $j^{th}$ element, you would do ~ $\log j$ comparisons and (in the worst case) ~$j$ shifts.

Summing over $j$, you get

$$ \sum_{j = 1}^{n} (j + \log j) = \frac{n(n+1)}{2} + \log (n!) = O(n^2 + n \log n) = O(n^2) $$

The idea is that the linear work of shifting trumps the logarithmic work of comparing. You end up doing less comparisons, but still a linear amount of work per iteration. So the complexity does not change.

Answer 2

The "possible explanation" after the edit in the question is exactly correct. That's why the time complexity is not improved.

On the other hand, unless the array is already mostly sorted, or if the array is very small, using binary search to find where to insert an array element is very likely to make the sorting almost twice as fast.

On the other hand, for large n where sorting an array using insertion sort is unacceptably slow, making it twice as fast still leaves it unacceptably slow.

Answer 3

I don't think the complexity is remain the same. Time complexity of binary insertion sort, if optimized the code

Sample Link: https://cboard.cprogramming.com/cplusplus-programming/139831-analysis-binary-insertion-sort-algorithm.html. My code to work with in Python: implement numpy for closer view at C/C++:

It is True that when you perform shifting element, it is always in linear way. However, even in the worse case, you re-defined the data at the remaining array without making any shifting but rather losing your time. Note that I want to clarify REAL-TIME Complexity; not Time Complexity in general to be more specific

Denote index at the outer is 'i'. Denote index from searching is 'j'

• If performing Linear Search for index && Full-scale Shifting (to the end): O(2N), which resulting O(2N^2) time complexity

• If performing Binary Search for index && Full-scale Shifting (Re-writing the array: O(N + log2(N)), which resulting O(N^2 + N*logN) time complexity

• If performing Binary Search for index && One-sided Shifting (to the end): O(N + log2(N)), which resulting O(N^2/2 + N*logN) time complexity

• If performing Binary Search for Index && Mid-bounded Shifting (to the "i" instead array.length). Time complexity in the worst case can be defined as follow:

• Binary Search: log2(N) : easy to determine
• However, in case of partially-shifting: Time complexity is O(k). Since you only shifting "i-j-1" variables by one move and re-adding the key-point "1". For relatively large array, in average case the number of shifting when k towards the left-half of the sorted one is equal to the right-helf of the sorted one. Thus causing O(i-j) = O(i//2) of time complexity. It can be viewed as using pivot in selection sort or quicksort or timsort.

Thus the overall time complexity for one epoch is log2(N) + i-j ~ log2(N) + i/2 Since this time, it can only be run up to N/2.

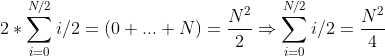
=> Time complexity for the whole array, in best case, O(N), near-asymtomtic case / small array is O(NlogN) and in average case, would be O(NlogN + N^2/4). If lucky enough, it could be O(NlogN + N^2/16) For best case and average case, it would be O(N) and O(2Nlog(N))

Take:

import numpy as np
import pandas as pd
from time import time
from typing import List
class Sorting:
    def init(self, data_size: int, lower_bound: int = 0, higher_bound: int = 1000):
        if lower_bound > higher_bound:
            lower_bound, higher_bound = higher_bound, lower_bound
    if data_size <= 0:
        self.__data__: np.ndarray = None
    else:
        using = max(abs(lower_bound), abs(higher_bound))
        if lower_bound == 0 and higher_bound > 0:
            x = [2 ** 8 - 1, 2 ** 16 - 1, 2 ** 32 - 1, 2 ** 64 - 1]
            dtype = [np.uint8, np.uint16, np.uint32, np.uint64]
        else:
            x = [2 ** 7 - 1, 2 ** 15 - 1, 2 ** 31 - 1, 2 ** 63 - 1]
            dtype = [np.int8, np.int16, np.int32, np.int64]

        for i in range(len(x)):
            if using <= x[i]:
                self.__data__ = np.random.randint(low=lower_bound, high=higher_bound,
                                                  dtype=dtype[i], size=data_size)
                break

    self.data_size: int = data_size
    self.lower_bound: int = lower_bound
    self.higher_bound: int = higher_bound

    self.columns: List[str] = ["Bubble Sort", "Selection Sort", "Insertion Sort (Min-Max)",
                               "Insertion Sort (Max-Min)", "Binary Insertion Sort"]
    self.recording_time: List[float] = [[0] * len(self.columns)]
    self.array_size = [data_size]

def reset_data(self, data_size: int, lower_bound: int = 0, higher_bound: int = 1000):
    # Avoid Memory Leakage
    del self.__data__
    if lower_bound > higher_bound:
        lower_bound, higher_bound = higher_bound, lower_bound

    using = max(abs(lower_bound), abs(higher_bound))
    if lower_bound == 0 and higher_bound > 0:
        x = [2 ** 8 - 1, 2 ** 16 - 1, 2 ** 32 - 1, 2 ** 64 - 1]
        dtype = [np.uint8, np.uint16, np.uint32, np.uint64]
    else:
        x = [2 ** 7 - 1, 2 ** 15 - 1, 2 ** 31 - 1, 2 ** 63 - 1]
        dtype = [np.int8, np.int16, np.int32, np.int64]
    for i in range(len(x)):
        if using <= x[i]:
            self.__data__ = np.random.randint(low=lower_bound, high=higher_bound,
                                              dtype=dtype[i], size=data_size)
            break

    self.data_size: int = data_size
    self.lower_bound: int = lower_bound
    self.higher_bound: int = higher_bound

    self.array_size.append(data_size)
    self.recording_time.append([0] * len(self.columns))

def get_array(self):
    return self.__data__

def sort_array(self):
    self.__data__.sort()

def reverse_array(self):
    self.__data__ = np.flip(self.__data__)

def BubbleSort(self, reverse: bool = False, copy: bool = True):
    """
    This method do bubble sort. Time complexity: O(N^2) since there are two loops over loops
    Real Time complexity: N*(N-1)/2
    :param copy: bool
    :param reverse: bool
    :return:
    """
    start = time()
    if copy is True:
        copied_version = np.copy(self.__data__)
    else:
        copied_version = self.__data__

    if reverse is False:
        for i in range(0, copied_version.size):
            swapped = False
            for j in range(len(copied_version) - 1, i, -1):
                if copied_version[j - 1] > copied_version[j]:
                    copied_version[j - 1], copied_version[j], swapped = copied_version[j], copied_version[j - 1], True
            if swapped is False:
                break

    else:
        for i in range(0, copied_version.size):
            swapped = False
            for j in range(len(copied_version) - 1, i, -1):
                if copied_version[j - 1] < copied_version[j]:
                    copied_version[j - 1], copied_version[j], swapped = \
                        copied_version[j], copied_version[j - 1], True
            if swapped is False:
                break

    end = time()

    self.recording_time[self.array_size.index(self.data_size)][0] = end - start
    print("Bubble Sort: Executing Time: {:.6f}s".format(end - start))
    return copied_version, end - start

def SelectionSort(self, reverse: bool = False, copy: bool = True):
    """
    This method do selection sort. Time complexity: O(N^2) since the first loop to iterate over the array.
    The second loop at "argmin" method which only return the first index that is smallest
    :param copy: bool
    :param reverse: bool
    :return:
    """

    start = time()
    if copy is True:
        copied_version = np.copy(self.__data__)
    else:
        copied_version = self.__data__

    if reverse is False:
        for index in range(0, copied_version.size):
            if index + 1 == copied_version.size:
                break
            minimum_index = index + 1 + copied_version[index + 1:].argmin(axis=-1)
            copied_version[index], copied_version[minimum_index] = \
                copied_version[minimum_index], copied_version[index]
    else:
        for index in range(0, copied_version.size):
            if index + 1 == copied_version.size:
                break
            minimum_index = index + 1 + copied_version[index + 1:].argmin(axis=-1)
            copied_version[index], copied_version[minimum_index] = \
                copied_version[minimum_index], copied_version[index]
    end = time()

    self.recording_time[self.array_size.index(self.data_size)][1] = end - start
    print("Selection Sort: Executing Time: {:.6f}s".format(end - start))
    return copied_version, end - start

def __BinarySearch__(self, array, number, start, end, reverse: bool = False):
    """
    This method will determine the accurate position to help sorting the array.
    Embedding with InsertionSort
    """
    if reverse is False:
        if start == end:
            if array[start] > number:
                return start
            else:
                return start + 1
    else:
        if start == end:
            if array[start] < number:
                return start
            else:
                return start + 1

    if start > end: # Ensuring position can be found
        return start

    mid = (start + end) // 2
    if reverse is False:
        if array[mid] < number:
            return self.__BinarySearch__(array=array, number=number, start=mid + 1, end=end, reverse=reverse)
        elif array[mid] > number:
            return self.__BinarySearch__(array=array, number=number, start=start, end=mid - 1, reverse=reverse)
        else:
            return mid
    else:
        if array[mid] > number:
            return self.__BinarySearch__(array=array, number=number, start=mid + 1, end=end, reverse=reverse)
        elif array[mid] < number:
            return self.__BinarySearch__(array=array, number=number, start=start, end=mid - 1, reverse=reverse)
        else:
            return mid

def InsertionSort(self, reverse: bool = False, copy: bool = True, perform_type: str = "binary"):
    """
    This method do insertion sort. Time complexity: O(N^2) since the first loop to iterate over the array.
    The second will have to pass the array to have the right order which thus getting O(k) complexity.
    Since k is iterate along with N, Real-time complexity is O(N^2)
    The second loop at "argmin" method which only return the first index that is smallest got O(N) complexity

    You can try binary insertion sort: it can help faster in sorting and lower down a little bit of time
    but general time complexity is remained. Time complexity in average case equal to O(N^2)
    """

    start = time()
    if copy is True:
        copied_version = np.copy(self.__data__)
    else:
        copied_version = self.__data__
    if perform_type.lower() == "left-right":
        left_to_right, right_to_left, binary = True, False, False

    elif perform_type.lower() == "right-left":
        left_to_right, right_to_left, binary = False, True, False

    elif perform_type.lower() == "binary":
        left_to_right, right_to_left, binary = False, False, True

    else:
        raise ValueError("Unable to found valid number")

    if reverse is False and left_to_right is True:
        for index in range(1, copied_version.size):
            key_point = np.copy(copied_version[index])
            if copied_version[index - 1] < key_point:
                continue
            for i in range(0, index):
                if i == 0:
                    if key_point < copied_version[i]:
                        copied_version[i + 1:index + 1] = copied_version[i:index]
                        copied_version[i] = key_point
                        break
                else:
                    if copied_version[i - 1] <= key_point <= copied_version[i]:
                        copied_version[i + 1:index + 1] = copied_version[i:index]
                        copied_version[i] = key_point
                        break

    elif reverse is False and right_to_left is True:
        for index in range(1, copied_version.size):
            key_point = np.copy(copied_version[index])
            if copied_version[index - 1] < key_point:
                continue
            i = index - 1
            while i >= 0 and key_point < copied_version[i]:
                copied_version[i + 1] = copied_version[i]
                i -= 1
            copied_version[i + 1] = key_point

    elif reverse is True and left_to_right is True:
        for index in range(1, copied_version.size):
            key_point = np.copy(copied_version[index])
            if copied_version[index - 1] > key_point:
                continue
            for i in range(0, index):
                if i == 0:
                    if key_point > copied_version[i]:
                        copied_version[i + 1:index + 1] = copied_version[i:index]
                        copied_version[i] = key_point
                        break
                else:
                    if copied_version[i - 1] >= key_point >= copied_version[i]:
                        copied_version[i + 1:index + 1] = copied_version[i:index]
                        copied_version[i] = key_point
                        break

    elif reverse is True and right_to_left is True:
        for index in range(1, copied_version.size):
            key_point = np.copy(copied_version[index])
            if copied_version[index - 1] > key_point:
                continue
            i = index - 1
            while i >= 0 and key_point > copied_version[i]:
                copied_version[i + 1] = copied_version[i]
                i -= 1
            copied_version[i + 1] = key_point
    else:
        for index in range(1, copied_version.size):
            key_point = np.copy(copied_version[index])
            if reverse is True and copied_version[index - 1] > key_point:
                continue
            elif reverse is False and copied_version[index - 1] < key_point:
                continue
            i = self.__BinarySearch__(array=copied_version, number=key_point, start=0, end=index - 1,
                                      reverse=reverse)
            copied_version[i + 1:index + 1] = copied_version[i:index]
            copied_version[i] = key_point
    end = time()
    if left_to_right is True:
        self.recording_time[self.array_size.index(self.data_size)][2] = end - start
    if right_to_left is True:
        self.recording_time[self.array_size.index(self.data_size)][3] = end - start
    if binary is True:
        self.recording_time[self.array_size.index(self.data_size)][4] = end - start
    print("Insertion Sort: Executing Time: {:.6f}s".format(end - start))
    return copied_version, end - start

def get_time(self, output: str = None):
    file = pd.DataFrame(data=self.recording_time, index=self.array_size, columns=self.columns)
    if output is not None:
        file.to_csv(path_or_buf=output)
    return file

def automate(self, size: List[int], lower_bound: int = 0, higher_bound: int = 1000, reverse: bool = False,
             insert_type: str = 'binary', bubble_sort: bool = True, selection_sort: bool = True,
             insertion_sort: bool = True, output: str = None):
    for index, value in enumerate(size):
        print("Matrix Size:", value)
        self.reset_data(data_size=value, lower_bound=lower_bound, higher_bound=higher_bound)
        # print(self.get_array())
        if bubble_sort is True:
            self.BubbleSort(reverse=reverse)
        if selection_sort is True:
            self.SelectionSort(reverse=reverse)
        if insertion_sort is True:
            self.InsertionSort(reverse=reverse, perform_type=insert_type)
    self.get_time(output=output)

My final word is optimize your code to lower down your REAL-TIME complexity rather make full attention on time complexity to think of.

[EDIT]: Real-Time complexity I will try to clarify this according to time-complexity in descending order:

• Linear Search + Array Rewriting:

Worst Case = Average Case: O(N) * O(N + N) = O(2N^2) (contained some "if" to get best case O(N))

• Linear Search + Element-Swapping:

Average Case: O(N) * O(N + N) = O(2N^2) (contained some "if" to get best case O(N))

Worst Case: could be O(N^3+N^2)

• Linear Search + Half-Right Swapping:

Worst Case: O(N) * O(N + N/2) = O(3/2 * N^2) (inversely-linear order, obtained by averaging left to right)

• Linear Search + Pivot ("j"-index) <--> Key ("i"-index) Swapping:

Worst Case: O(N) * O(N + N/4) = O(5/4 * N^2) (inversely-linear order:, obtained by averaging left to right)

Average Case: O(N) * O(N + N/16) = O(16/15 * N^2) (inversely-linear order, obtained by averaging left to right)

• Binary Search + Array Rewriting:

Worst Case = Average Case: O(N) * O(log2(N) + N) = O(N^2 + Nlog2(N)) (contained some "if" to get best case O(N))

• Binary Search + Element Swapping:

Average Case: O(N) * O(log2(N) + N) = O(N^2 + Nlog2(N)) (contained some "if" to get best case O(N))

Worst Case: O(N^3 + Nlog2(N))

• Binary Search + Half-Right Swapping:

Worst Case = Average Case: O(N) * O(log2N + N/2) = O(1/2 * N^2 + Nlog2(N)) (inversely-linear order, obtained by averaging left to right)

• Binary Search + Pivot ("j"-index) <--> Key ("i"-index) Swapping:

Worst Case: O(N) * O(log2(N) + N/4) = O(1/4 * N^2 + Nlog2(N)) (inversely-linear order:, obtained by averaging left to right)

Average Case: O(N) * O(log2(N) + N/16) = O(1/16 * N^2 + Nlog2(N)) (inversely-linear order:, obtained by averaging left to right)

Lucky Case: O(2Nlog2(N))