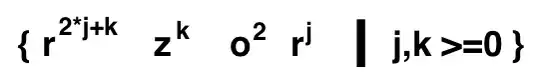A couple of things:
Sometimes it helps to simplify the description of your grammar. Instead of $\{r^{2j+k}j^ko^2r^j \mid j,k \geq 0 \}$, you can write this: $\{r^{2j}r^kj^koor^j \mid j,k \geq 0\}$. It is still the same grammar, but you can easier see what you're doing. For example, something here stands out: $\{r^{2j}\mathbf{r^k}\mathbf{j^k}oo\mathbf{r^k} \mid j,k \geq 0\}$
Next: Sanity-checking. See if what you're trying to achieve conflicts with any known rules. Can this language be produced by a context-free grammar? Or is this language not context-free? Consider that $\{ a^kb^kc^k \mid k \geq 0\}$ is a classical example for non-context-free grammars (It is context sensitive).
If the language is not context-free, we can stop trying to find a context-free grammar for it. Attempts will be (hopefully) futile.
Unfortunately, I can't provide you with a simple way of constructing grammars for context-free languages. Maybe (probably) some other (far more experienced and knowledgeable) members here might be able to do so. What worked for my (short) stint in TCS, practice helped. I started with simple examples, and increased their complexity. Then you learn to recognize some patterns in languages and solve them for example by splitting the language into multiple, smaller and simpler languages which you already know how to solve.
Lets try to apply that to this case: $\{r^{2j}r^kz^koor^j \mid j,k\geq0\}$
We can see that that is essentially $\{r^{2j}$ [something else] $r^j \mid j\geq0\}$. That is easy to produce:
$S \rightarrow rr X r | X$, where $X$ will produce the [something else].
That something else is of course $r^kz^koo \mid k\geq0$, which is also easy to produce:
$X \rightarrow Y oo | oo$ and
$Y \rightarrow rYz$
Ultimately, the key behind this construction was simplifying the language, and then recognize that the language is a nested variation of $\{a^k\ b\ a^k\}$ and $\{a^k\ b^k\ a\}$, which both are trivial languages to produce.