2

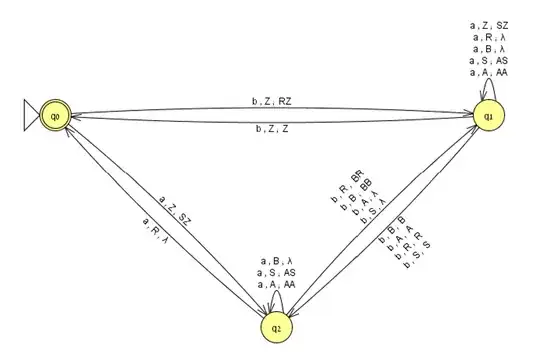
I've been studying Computation Theory, and in an exercise I am asked to construct a PDA that accepts the language $L=\{x\in(a,b), \#_a(x) = 2\#_b(x)\}$, where $x$ is the input string and $\#_a(x),\#_b(x)$ the number that $a$ or $b$ appears in the $x$ string.

That means that the following sequences should all be accepted:

aab aba bbaabaaaa baabaa abbaaa

My problem: I've found examples of PDAs being constructed for $a^nb^n$ and even $a^{2n}b^n$ which is pretty close to what I'm looking for, but these languages all have a predetermined sequence of the $a$s coming first, then the $b$s.

I've been trying for literally hours to build a PDA that circles between how many $a$s and $b$s it has, and how many it still needs, but every attempted solution has been wrong (situations where consequent same letters cause pops on empty stacks, halting the PDA).

Any information or methodical approaches on constructing a PDA out of a language like that? I'm at my wit's end.

Raphael
  • 73,212
  • 30
  • 182
  • 400
Dimitris Sfounis
  • 225
  • 2
  • 9

2 Answers2

1

GPDA$\to$PDA Approach

See you have got a solution from chat. But the first thing popped my mind is a Generalized_pushdown_automaton(GPDA), which can be constructed pretty straight forward.

GPDA construction

$M=(Q,\Sigma,\Gamma,\delta,q_0,Z,\{q_f\})$, where $Q=\{q_0,q_f\},\Sigma=\{a,b\},\Gamma=\{a,A,Z\}$,$\delta$ includes following rules:

  1. $(q_0,a,Z)\to(q_0,aZ)$
  2. $(q_0,b,Z)\to(q_0,AAZ)$
  3. $(q_0,a,a)\to(q_0,aa)$
  4. $(q_0,b,A)\to(q_0,AAA)$
  5. $(q_0,a,A)\to(q_0,\epsilon)$
  6. $(q_0,b,aa)\to(q_0,\epsilon)$
  7. $(q_0,b,aZ)\to(q_0,AZ)$
  8. $(q_0,\epsilon,Z)\to(q_f,\epsilon)$

GPDA$\to$PDA convertion

Using the algorithm provided on Wikipedia, we can convert it to PDA easily. Only 6. and 7. need to convert:

6.1 $(q_0,b,a)\to(p_0,\epsilon)$

6.2 $(p_0,\epsilon,a)\to(q_0,\epsilon)$

7.2 $(p_0,\epsilon,Z)\to(q_0,AZ)$

Resulting PDA is $M=(Q',\Sigma,\Gamma,\delta',q_0,Z,\{q_f\})$ where $Q'=\{q_0,p_0,q_f\}$ and $\delta'=(\delta\setminus\{6,7\})\cup\{6.1,6.2,7.2\}$. The constructed PDA is non-deterministic.

Convert to DPDA

To convert to DPDA, the only affected transitions are 1. 2. and 8 in above rules:

$M=(Q,\Sigma,\Gamma,\delta,q_0,Z,\{q_f\})$, where $Q=\{q_0,p_0,q_f\},\Sigma=\{a,b\},\Gamma=\{a,A,Z\}$,$\delta$ includes following rules:

  1. $\mathbf{(q_0,\epsilon,Z)\to(q_f,Z)}$
  2. $(q_0,a,a)\to(q_0,aa)$
  3. $(q_0,b,A)\to(q_0,AAA)$
  4. $(q_0,a,A)\to(q_0,\epsilon)$
  5. $(q_0,b,a)\to(p_0,\epsilon)$
  6. $(p_0,\epsilon,a)\to(q_0,\epsilon)$
  7. $(p_0,\epsilon,Z)\to(q_0,AZ)$
  8. $\mathbf{(q_f,a,Z)\to(q_0,aZ)}$
  9. $\mathbf{(q_f,b,Z)\to(q_0,AAZ)}$
Terence Hang
  • 789
  • 4
  • 7
0

enter image description here

This is a solution for this problem I built in JFLAP

Vunag
  • 1
  • 1