The tree traversal methods explained in this Wikipedia article are pre-order, post-order and in-order. Are these methods limited to binary trees? The algorithm seems to be defined in terms of left and right child. If it can be used for n-ary trees, how?
An n-ary tree has 1 parent and n children at any given node. Where n can be any whole number for each node.
Please use the figure below to explain this, if you need one.
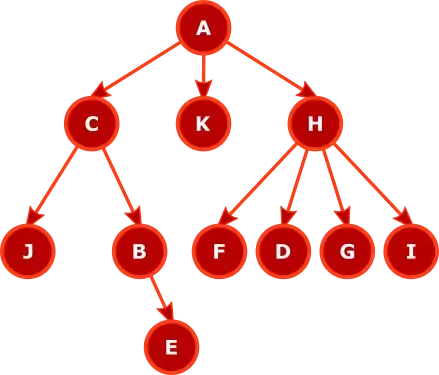
No, it's not limited to binary trees. Yes, pre-order and post-order can be used for $n$-ary trees. You simply replace the steps "Traverse the left subtree.... Traverse the right subtree...." in the Wikipedia article by "For each child: traverse the subtree rooted at that child by recursively calling the traversal function". We assume that the for-loop will iterate through the children in the order they are found in the data-structure: typically, in left-to-right order, for a diagram such as you have shown.
In fact, this is already described in the Wikipedia article on tree traversals: see https://en.wikipedia.org/wiki/Tree_traversal#Generic_tree, which describes exactly how to generalize this to $n$-ary trees. Pre-order traversal is one where the pre-order operation is "Display the current node" and the post-order operation is "Do nothing". Post-order traversal is one where the pre-order operation is "Do nothing" and the post-order operation is "Display the current node".
In-order traversal is a special case. It probably only makes sense for binary trees. While there are several different possible ways that one could define in-order traversal for $n$-ary trees, each of those feels a bit odd and unnatural and probably not terribly useful in practice. So, it's probably best to think of in-order traversal as being specific to binary trees; if you want to do something akin in-order traversal for a $n$-ary tree, you'll need to decide exactly what you mean by that, as there's no standard meaning for that.
There are many exotic data structures used all over CS with many variants. There was some similar recent question (now deleted) about traversing n-ary trees in an ordered way by overexchange. It appears that most or many n-ary trees in the literature studied tend not to be ordered. However, as an alternative pov / exceptional / "edge" case on the other detailed answer, there are cases of ordered n-ary trees that are not "odd and unnatural and probably not terribly useful in practice". Here is one ref; there are likely many other cases, although it's possible they are not in widespread use.
[1] n-ary ordered trees / P Mateti 7140 course notes
