Hamiltonian circuit for a family of graphs

Question

For $\Sigma = \{a,b\}$, let $S_n = \{w\mid w \in \Sigma^{*} \land |w| = n\}$.

Let $C_n \subset \Sigma^{*}$ be the language of circular strings that contain as substrings all elements of $S_n$. For instance, $bbaaaababaabbbba \in C_4$

I have formulated the problem of finding the subset of $C_n$, formed by the circular strings with the smallest size ($=2^n$), as the problem of finding all hamiltonian circuits on the graph that has the elements of $S_n$ as vertices, and edges connecting all pairs of vertices $s_i$ and $s_j$ such that $s_i = xw$ and $s_j = wy$, with $w \in \Sigma^{n-1}$ and $x,y \in \Sigma$.

For the example above, the graph could look like this:

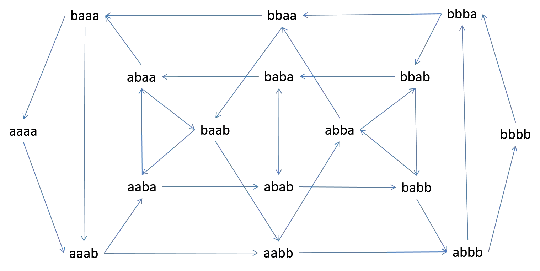
My question:

Would there be a polynomial-time solution for the hamilton circuit problem restricted to this family of graphs?

Answer 1

This graph is known as a de Bruijn graph, and its Hamiltonian circuits are known as de Bruijn sequences. Both are well understood (for example, we know exactly how many of these exist).