I have a tetrahedron $t$ and a polyhedron $p$. $t$ is constrained such that it always shares all its vertices with $p$. I want to determine whether $t$ lies inside $p$.
I would like to add one detail to the problem in case it may contribute to the solution: $t$ is a Delaunay tetrahedron and faces of $p$ are triangular and are strongly Delaunay both with respect to vertices of $p$. A tetrahedron is Delaunay if circumsphere of its vertices contains no other vertex inside it. A face is strongly Delaunay if there exists a circumsphere containing vertices of that face on its surface but no other vertex on or inside it.
Following figures show the same problem in $2D$ space:
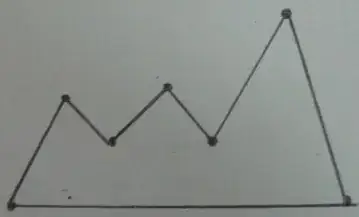
The original polygon $p$:
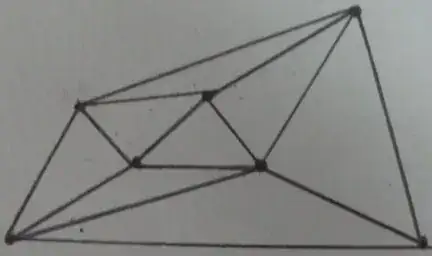
Delaunay triangulation of vertices of $p$:
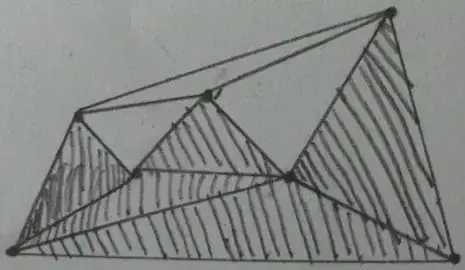
Result of inside/outside test over triangles $t$(Shaded triangles are inside $p$ and rest are outside):
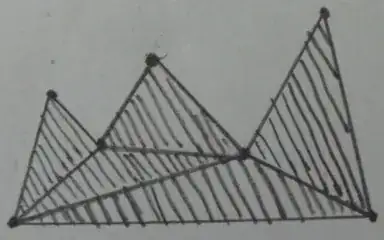
Desired result(pruning outside triangles):
My original problem is in 3D space so triangles $t$ in above figures translate to tetrahedrons and polygon $p$ translates to an arbitrary polyhedron $p$. I have figured out some formulations of this problem:
Formulation 1
The only parts of $t$ which can be outside $p$ are its edges and triangular faces but in general there may exist a $p$ which has edges of all outside $t$'s on its surface, so alternatively, this problem may also be formulated as to test whether for a tetrahedron $t$ there exists a face which lies outside $p$?
Formulation 2
I have another possible perspective towards this problem but lacking any formal idea:
Geometrically, if $t$ is outside then it will always be sticking on the outer surface of $p$. So if we can compute the contours(informally, the outer boundary) $C_{V}$ and $C_{V_{p}}$ such that $V=V_{t}\cup V_{p}$ and $V_t,V_p$ are sets of vertices in $t,p$ respectively, then $C_{V}=C_{V_p}$ iff $t$ lies inside $p$.
I would like to know:
- How can I solve either of Formulation 1 or Formulation 2?
- Or, is there any completely different approach to solve this?
Update:
I now realize that this problem can be reduced to Point in polyhedron problem. Since an outside tetrahedron $t$ will have at least one face which lies outside $p$, so any arbitrary point on that face(except its vertices,in general) will always lie outside $p$. Therefore, for each face of $t$, I need to take an arbitrary point and test if that point lies outside $p$.
From point in polygon article I came to know about Ray casting algorithm and Winding number algorithm. Ray casting is not numerically stable for cases where point lies on the surface of $p$. But numerical robustness of Winding number algorithm has not been addressed there.
Based on above, my core problem now seems to be(please suggest if it should be asked as a separate question):
Is there any numerically robust algorithm for point in polygon problem?