Tree Search $A^*$ With an Admissible Heuristic Does Not Necessarily Return an Optimal Solution

Question

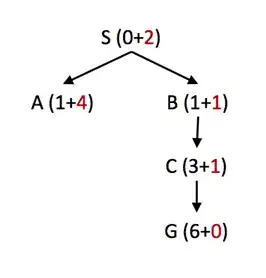
I know that the title of this post is wrong, but I got stuck on an example. Consider the graph below, which I obtained from here.

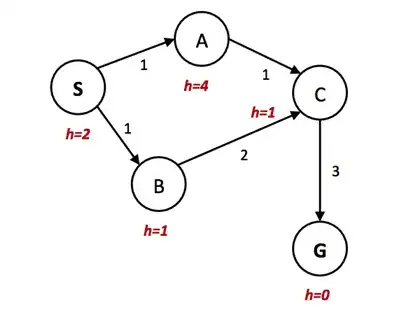
To the best of my knowledge, the tree search version of $A^*$ fails to provide the optimal path, even though the heuristic $h$ seems to be admissible. My search tree would look something like this:

The reason I stop after having found $G$ is because this is how I've seen tree-search algorithms being implemented or described. For example, here and here

which is taken from the book Artificial Intelligence - A Modern Approach. In pseudocode, we see that we return a solution as soon as we've found the goal state, which leads to the same issue seen here. What seems to fix this is that we don't return the moment we find a goal, but wait until we go through the whole queue. Do I have the right idea? Is the pseudo-code laid in the book, and the one from the stackoverflow site, inaccurate because of this?

Answer 1

This version of the algorithm works only if the heuristic is consistent, not only admissible (as you have found a counter-example).

Your heuristic isn't consistent, because, for example, $h(A) = 4 > h(C) + d(A, C) = 2$.

This is the version most often used, because its time complexity is polynomial in the size of the input.

It is possible to create an optimal algorithm for admissible-only heuristics, but you'd need to be able to mark vertices as unexplored each time a shorter path is found. It would result in an exponential time algorithm.

In your example, that would mean that after you find a path of weight $6$ from $S$ to $G$, you mark $G$ as unexplored, and the next vertices removed from the frontier would be $A$, as $h(A) + d(S, A) = 5 < 6$. From there, you'd be able to find the shortest path.

In fact, this is exactly what is done with Dijkstra's algorithm when the graph contains negative weight edges (and indeed, there is no known polynomial-time algorithm in this case).