1

I'm new to automata and in my first exercise I have to construct a DFA that starts with 'b' and length=3. Two symbols (a,b).

To my understanding, there are 4 possibilities {baa,bab,bba,bbb}

I have attached a picture showing where I got stuck. Any help is appreciated, also please tell me if the part I've already done has errors.

https://postimg.cc/7JPNyRVq

D.W.
  • 167,959
  • 22
  • 232
  • 500
Laz
  • 21
  • 2

2 Answers2

2

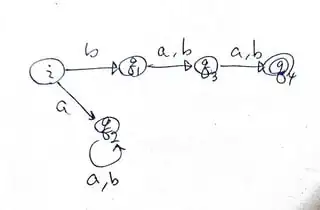
Hint 1: Every state in a DFA "remembers something", for example, in your attempt, the state $q_1$ remembers two things: (1) that we've just read $b$, and (2) that we've read a word of length 1 so far. Now if you want to accept all words whose length is exactly 3 and start with $b$, then:

1- What would you do from the state $q_1$ upon reading a letter?

2- What would you do from a state, to be added, that remembers that we have read a word that starts with $b$ and whose length is 3?

Hint 2 (more general): All words over $\Sigma = \{a, b \}$ of length $\leq k$ for some constant $k$, can be presented as a finite full binary tree whose depth is at most $k$, where the root corresponds to the empty word, and if a word node $n$ corresponds to a word $w$, then its left child and right child correspond to the words $wa$ and $wb$, respectively. Think how you can define a DFA for your language on top of that tree. In fact, this hint can be used to show that every finite language is regular.

Bader Abu Radi
  • 5,494
  • 1
  • 11
  • 41
0

How about creating an NFA with Thompson's construction, and getting the equivalent DFA with powerset construction? Here's how it goes:

First, a regular expression describing a language consisting strings with length of 3 and starting with $b$ would be $b(a|b)(a|b)$. Use Thompson's construction to get

NFA

In this case, the automaton is already deterministic, so therefore, powerset construction is not needed, and you got the automaton you want.

Nascity
  • 13
  • 5