A more concise Finite Automata for 10 substring?

Question

I am learning about finite automata and trying to create a machine that matches

{w ∈ Σ∗| w does not contain the substring 10}

I created a DFA where it either starts with 1 or 0. I know it's not the most concise FA, but is it accurate?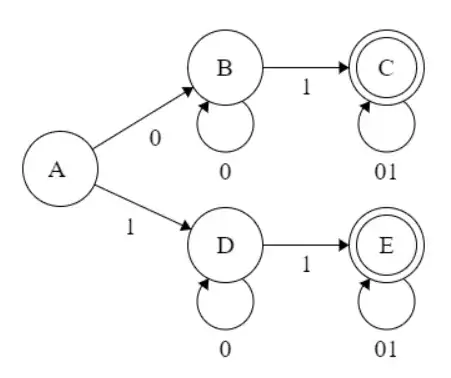

Answer 1

Your automaton (automata is the plural word) is wrong:

• as @Knogger stated, there is no initial state
• finite automata (unless generalized) can only have one-letter transitions, so transitions $01$ are not allowed
• even if $01$ transitions are allowed, this would create $10$ as substring, since $0101$ contains $10$.

You should try again, noting the fact that a word $w\in \{0,1\}^*$ does not contain $10$ as a substring if and only if $w = 0^p1^q$, for some $p, q\geqslant 0$.

Answer 2

This one is a classic textbook problem. You can build your required DFA as follows:

step 1: build a complete DFA $M$ that accepts all strings containing 10 as a substring

step 2: just swap the status of final/non-final states in this DFA to get another DFA $M'$

step 3: argue that $M'$ has to be your required one

Read more about DFA complementation here.