I have a bunch of values, some that are given by an end user input and some that are calculated based on that input. The way that the values are calculated are input by a different group of users of the software. My goal is to give the second group of users feedback that their input can always be solved.
Now to the actual CS problem:
Assume I have a dependency graph. Each of the nodes may either have a simple static value or a value that is calculated via some static values or by using values saved in other nodes (so no global state that can change). In this case, an acyclic graph means that in can always be solved while cycles mean it cannot be solved uniquely¹.
However, some of these nodes (let's call them conditional nodes) only require some of the dependencies depending on some condition. For example:
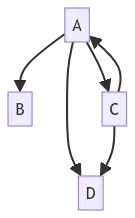
A --> B;
A --> C;
A --> D;
C --> A;
C --> D;
This dependency graph does have a cycle with A & C:
However, if A and C now have the following calculated values:
A: if B > 3 then C else D
C: if B < 1 then A else D
In this case, this set of values can always be uniquely solved:
| B | A | C |
|---|---|---|
| B > 3 | C = D | D |
| 1 <= B <= 3 | D | D |
| B < 1 | D | A = D |
I would now need a generic way to guarantee that the set of calculations can always be solved regardless of the actual "static" values input.
Is there an algorithm that would cover this problem?
While I originally started with a simple dependency graph, introducing these conditionals reminded me more of logic based programming languages and made me think of searching for algorithms within constraint logic programming. But this was the first time of me dabbling in that area and I've quite frankly not found a fitting algorithm as all of them seem to test specific input rather than validate for arbitrary input.
I'm also still very much in the conceptual & prototyping phase of the project so don't feel forced to use a dependency graph as underlying structure if it's unsuitable.
¹ For example A = B + 2. B = A - 2 can be solved in infinite ways, but I need exactly one unambiguous solution ignoring known mathematical problems like dividing by zero or limitations of modern computing like floating point arithmetic.