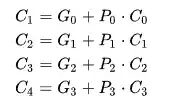How to construct a carry-lookahead adder of the optimal $O(n)$ size

Question

Problem (TL;DR): I'd like to know how to construct a CLA adder that has $O(n)$ size and $O(\log n)$ depth using only fan-in 2 AND gates and XOR gates, as suggested in this answer and this answer.

Settings and motivation: I am doing a research project where we need to add or subtract two $n$ bit strings in 2's completement representation. Specifically, I am working in the area of secure multiparty computation, where generally we express a function that we want to securely compute as a boolean circuit, and use some off-the-shelf "compiler" to "compile" such circuit into a secure protocol that can be executed between the parties without leaking information.

In our work, we care about two things: communication complexity and round complexity. It turns out that the aforementioned compiler requires $O(1)$ communication and $O(1)$ rounds to compute an AND gate and no communication or round to compute an XOR gate. We are only allowed to use these two types of gates but they are universal. Therefore, the communication complexity scales roughly with the size of the circuit and the round scales roughly with the depth of the circuit.

Constraints: Only fan-in 2 AND gates and XOR gates can be used.

My attempts: I understand how to do it in $O(\log n)$ depth, but the problem is that my carry-lookahead unit is too large in size, specifically, it is $O(n^2)$. I am looking at the following carry-lookahead formula from Wikipedia.

To compute $C_i$, we need to (at least) compute the $i$ OR's, which are just AND gates in disguise. Therefore, even we can compute the individual summands in constant size, it does not seem that I can get better than $O(n^2/2)$ because of the OR's. This implies that we must reuse computation in some clever way, and I've tried the work-efficient parallel prefixsum network or a segment-tree, none of which allowed me to cut these OR's or even just evaluates the individual summands efficiently.

I must be lacking some crucial insights here, after all, these expressions looks so temptingly recursive, but I've tried everything I can think of. I would appreciate either a fully worked-out solution or just a hint. Thanks for the helps in advance.

Answer 1

Actually, upon working on this problem for a bit more time, I discovered one method to build a size $O(n)$ and depth $O(\log n)$ CLA circuit. The key ingredient is the work-efficient parallel prefixsum network, e.g., as seen in the Blelloch scan. There, it is shown that using any associative binary operators in place of the normal addition, the prefixsum (using this binary operator) can be computed with a network of size $O(n)$ and depth $O(\log n)$.

Consider the problem at hand, we want to compute the following efficiently

If we define a function $f_{a, b}(x) := a + bx$, then we can write the above as $$\begin{aligned} C_1 &= f_{G_0, P_0}(C_0), \\ C_2 = f_{G_1, P_1}(C_1) &= (f_{G_1, P_1} \circ f_{G_0, P_0})(C_0), \\ C_3 = f_{G_2, P_2}(C_2) &= (f_{G_2, P_2} \circ f_{G_1, P_1} \circ f_{G_0, P_0})(C_0), \\ C_4 = f_{G_3, P_3}(C_3) &= (f_{G_4, P_4} \circ f_{G_2, P_2} \circ f_{G_1, P_1} \circ f_{G_0, P_0})(C_0).\end{aligned}$$

If we let $\circ$ be the function composition operator defined by $f_{a,b}(x) \circ f_{c,d}(x) = f_{c+ad, bd}(x)$, then it is easy to check that this operator is associative. We can either argue that it is so because function composition is in general associative, or explicitly check it as follows: $$(f_{a,b} \circ f_{c,d}) \circ f_{e,f} = f_{c+ad, bd} \circ f_{e,f} = f_{e+cf+adf, bdf},$$ $$f_{a,b} \circ (f_{c,d} \circ f_{e,f}) = f_{a,b} \circ f_{e+cf, df} = f_{e+cf+adf,bdf}.$$

Therefore, if we take our array to be $[f_{G_0, P_0}, f_{G_1, P_1}, f_{G_2,P_2}, f_{G_3,P_3}]$, taking the prefixsum on this array gives us an array $[\bigcirc_{i=0}^{k} f_{G_i, P_i}]$ for $0 \leq k \leq 3$, where $\bigcirc$ denotes repeated composition. Now, we only need to apply each item of this array to $C_0$ to get the array $[C_1, C_2, C_3, C_4]$. This completes the construction.

The Blelloch scan network guarantees us that we can implement the above prefixsum with $O(sn)$ size and $O(d\log n )$ depth, where $s$ and $d$ are the size and depth of the gate computing the composition, respectively. However, the composition only involves 2 AND gates and 1 OR gate, so its size and depth are both $O(1)$. Since the above easily generalize to any $n$ beyond $4$, we conclude that a $n$-bit CLA adder can be implemented with $O(n)$ size and $O(\log n)$ depth.