1

Case:1

Suppose l have one DFA which accepts the set of all strings over {a, b} which starts with aand it's complement is not starts with a.

enter image description here From the above image we see that in the second diagram represents the DFA which accepts the strings which belong to complement of the language accepted by first DFA.

Case:2

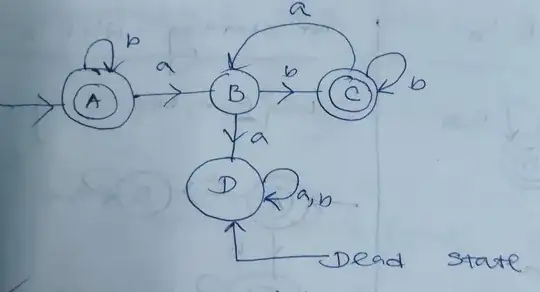
Now consider the DFA which accepts set of all strings over {a, b} in which every a is followed by b. And the language should be

L={$\epsilon$,ab,abab,....b,bb,...bab,bbab,babbbbab,....}

See the image:enter image description here

Now consider the DFA which accepts set of all strings over {a, b} in which every a should never followed by b(which is the complement of DFA which accepts set of all strings over {a, b} in which every a is followed by b.).

And the language should be

L'={$\epsilon$,a,aa,aaa,......b,bb,....ba,bba,bbba,....}

See the complement of L which is L':

enter image description here

In the last diagram we see that the DFA which accepts the strings like aab, aba etc which shows that language don't complemented of L properly.

My question is that in case:1 language, DFA and it's correspondence complement works properly. But in second case after complimenting DFA we don't get complimented language. Where did I mistaken to understand DFA and it's complement? Actually be L' represents the complement of L or not in case:2?

S. M.
  • 1
  • 4
  • 19

2 Answers2

2

Let $L$ be the language over the alphabet $\{a,b\}$ defined by $L = \{w: \mbox{an $a$ in $w$ is always followed by a $b$}\}$. Let $L' = \{w: \mbox{an $a$ in $w$ is never followed by a $b$}\}$. Observe that $L$ and $L'$ are not complements of each other. Strings such as $aab$ and $aba$ belong to neither $L$ nor $L'$ because some of the $a$'s in the string are followed by a $b$, but other $a$'s in the string are not followed by a $b$.

The strings $aab$ and $aba$ are not in $L$, and since you have a DFA for $L$, these strings are accepted by the complement DFA. It's just that your description of the complement $L'$ is incorrect. The complement of $L$ would be the language consisting of all strings $w$ over the alphabet $\{a,b\}$ such that $w$ contains at least one $a$ that is not followed by a $b$.

Ashwin Ganesan
  • 1,388
  • 7
  • 10
2

I have forgotten the quantifier:

~$\forall x \,(P(x))\neq$$\forall x \,($~$P(x)).$ Instead

  1. ~($\forall x \,,P(x))= $$(\exists x \,,$~$P(x))$.

  2. ($\forall x \,,$~$P(x))= $~$(\exists x \,,P(x))$.

That means Complement of $a$ always followed by $b$ is not $a$ never followed by $b$ instead:

  1. Complement of $a$ always followed by $b$ is at least one $a$ is not followed by $b$ in any strings.
  2. $a$ is never followed by $b$ is complement of at least one $a$ is followed by $b$ in any strings.
S. M.
  • 1
  • 4
  • 19