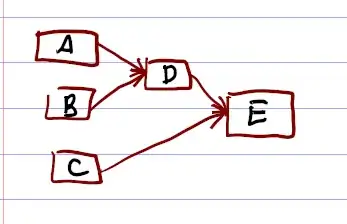
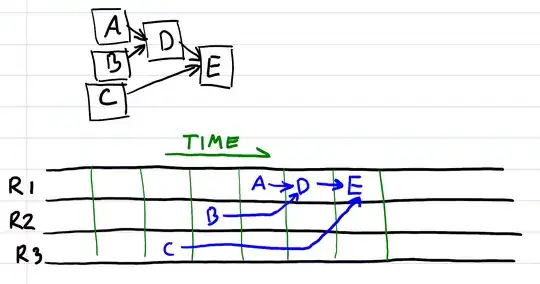
A common way to resolve a dependency graph is to compute an execution order, and then execute each stage in turn - storing and fetching the resources as necessary. In this example, when executing stage E we know that stage B is present in the cache due to the execution order. At the end of execution, the output of every operation is present in the cache.

This works fine if your cache is big enough to store the output of every result in the graph, but this is not always true. In my case the number of operations may approach 10,000 or so (brush strokes in a painting for the curious), and the number of items that can be stored in the cache is perhaps 100 or so (textures in the GPU). Fortunately the graph has lots of chains, so should be solvable.
There are at (so far) three questions that come out of this situation:
1) How to compute an execution order?
Given that the cache is of finite size, not all execution orders are valid. Imagine that we only have two available resources and consider:
If we try execute B and C (both of which can be computed immediately), then we get stuck because we cannot compute A due to lack of resources, and we cannot compute D or E due to unfulfilled dependencies.
Operation: B | C | A | ?
------------------------------>
In Cache: | B |B,C| ??
Of course, if we execute A -> B -> D -> C -> E then we can complete execution of the graph. (The outputs of A and B can be removed after D is computed etc.).
Operation: A | B | D | C | E
--------------------------------->
In Cache: | A |A.B| D |C,D| E
^
|
Removed A and B to make room for D
This implies that an ad-hoc iterative implementation (for each node check if all it's dependencies are ready, and if so, run it) will not function in cases where resources are low.
So, how can I derive an execution order that is optimized for the lowest number of resources to be allocated at any given time?
2) How to count how many resources are required for graph execution?
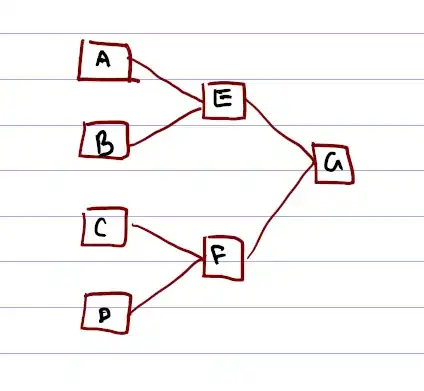
Evidently there is some limit to if a graph is computable with a provided amount of resource. For example the first graph requires three resources, and the second one requires at least two. In those cases that is because one of the nodes has that many inputs. But this isn't always the case. Consider:
In this case every node has only two inputs, but execution of the graph requires three resources.
I guess this is highly related to actually solving the graph, but it may be separable. Either way it is nice to say "this long an expensive system graph that will take 6 hours to run will successfully complete and not run out of resources half way through"
3) How to tell when a resource can be removed from the cache
I guess one approach is to have each item in the cache count how many times it has been used, and when that number is equal to the number of dependants, it can be removed. But it would be nice to compute two associated arrays: one that describes the order of operations to execute, and another that describes, for each operation, which items in the cache are no longer required.
4) Are there any existing resources/studies on solving this problem?
I've had a look through some books on graph theory and done some browsing of the web, but haven't found any resources that describe this problem. It is likely that I don't know the terminology involved, so suggesting some reading is welcome. In fact, I would love it if someone says "It's known as problem x and there are dozens of papers on the topic"