Does the Linz Ĥ applied to ⟨Ĥ⟩ correctly transition to its final reject state?

Question

// Linz Turing machine H --- H applied to ⟨H⟩ 
H.q0 ⟨H⟩ ⟨H⟩ ⊢* H.qy   // H applied to ⟨H⟩ halts
H.q0 ⟨H⟩ ⟨H⟩ ⊢* H.qn   // H applied to ⟨H⟩ does not halt
Do you halt on your own Turing Machine description ?

Of the infinite set of implementations of H every one that transitions to H.qy derives an answer consistent with the behavior of H.

When we append an infinite loop to the H.qy state we derive Ȟ

Ȟ.q0 ⟨Ȟ⟩ ⟨Ȟ⟩ ⊢* Ȟ.qy ∞ // Ȟ applied to ⟨Ȟ⟩ halts
Ȟ.q0 ⟨Ȟ⟩ ⟨Ȟ⟩ ⊢* Ȟ.qn   // Ȟ applied to ⟨Ȟ⟩ does not halt 
Do you halt on your own Turing Machine description ?

Of the infinite set of implementations of Ȟ none of them derives an answer consistent with the behavior of Ȟ.

This is because the question:
Do you halt on your own Turing Machine description ?
is self-contradictory thus incorrect question for Ȟ.

Yes/no questions intentionally defined to have no correct yes/no answer are incorrect questions. The inability to correctly answer an incorrect question places no actual limit on anyone or anything.

Two PhD computer science professors agree with this view:

E C R Hehner. Objective and Subjective Specifications WST Workshop on Termination, Oxford. 2018 July 18. See https://www.cs.toronto.edu/~hehner/OSS.pdf

Bill Stoddart. The Halting Paradox 20 December 2017 https://arxiv.org/abs/1906.05340 arXiv:1906.05340 [cs.LO]

Prior question

Applying a Simulating Halt Decider to the Linz Halting Problem Proof

A simulating (at least partial) halt decider correctly predicts whether or not its correctly simulated input can possibly reach its own final state and halt. It does this by correctly recognizing several non-halting behavior patterns in a finite number of steps of correct simulation. Inputs that do terminate are simply simulated until they complete.

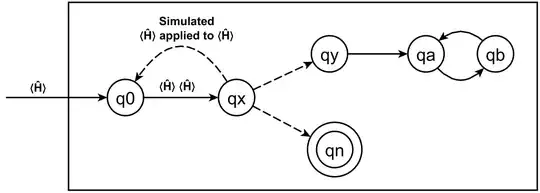
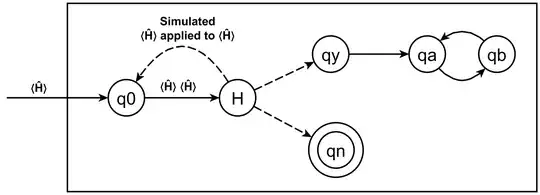
The Linz text indicates that Ĥ is defined on the basis of prepending and appending states to the original Linz H, (assumed halt decider) thus is named embedded_H.

(q0) is prepended to H to copy the ⟨Ĥ⟩ input of Ĥ. The transition from (qa) to (qb) is the conventional infinite loop appended to the (qy) accept state of embedded_H. ⊢* indicates an arbitrary number of moves.

The Linz term “move” means a state transition and its corresponding tape head action {move_left, move_right, read, write}. Ĥ is applied to its own machine description ⟨Ĥ⟩.

Ĥ.q0 ⟨Ĥ⟩ ⊢* embedded_H ⟨Ĥ⟩ ⟨Ĥ⟩ ⊢* Ĥ.qy ∞
Ĥ.q0 ⟨Ĥ⟩ ⊢* embedded_H ⟨Ĥ⟩ ⟨Ĥ⟩ ⊢* Ĥ.qn

When Ĥ is applied to ⟨Ĥ⟩
(q0) The input ⟨Ĥ⟩ is copied then transitions to (qx)
(qx) embedded_H is applied to ⟨Ĥ⟩ ⟨Ĥ⟩ (input and copy)
which simulates ⟨Ĥ⟩ applied to ⟨Ĥ⟩ which begins at its own (q0) to repeat the process.

This process continues to repeat until embedded_H recognizes the repeating pattern and aborts its simulation of ⟨Ĥ⟩ ⟨Ĥ⟩. embedded_H can see the same repeating pattern that we see.

computation that halts… “the Turing machine will halt whenever it enters a final state” (Linz:1990:234)

Every "rebuttal" simply ignores this key fact

⟨Ĥ⟩ ⟨Ĥ⟩ correctly simulated by embedded_H cannot possibly reach its own simulated final state of ⟨Ĥ.qn⟩ and halt in any finite number of steps of correct simulation.

Linz, Peter 1990. An Introduction to Formal Languages and Automata. Lexington/Toronto: D. C. Heath and Company. (317-320)

Answer 1

This is an answer to an attempt at understanding a previous version of the question, and is no longer relevant to the latest question.

---

Your question is: What happens when you use a simulating halt decider and (...)?

The answer is: You can't. The question has a faulty premise. A simulating halt decider does not exist, so there is no meaningful answer to the question.

---

I'll highlight your definition. You propose the following definition:

A simulating (at least partial) halt decider H is a UTM that has been adapted to decide whether or not its input halts. It does this by simulating its input and examining the behavior of this simulated input.

(I presume this should be interpreted as saying that, to count as a simulating halt decider, the UTM must always correctly decide whether or not its input halts, for all possible inputs.)

The problem is: there does not exist any UTM that successfully acts as a simulating halt decider on all inputs.

You can add all the conditions and requirements you want to a definition. The definition remains valid. But there is no guarantee that there exists any object that meets the conditions of the definition. That has to be separately verified.

It sounds like you think that there does exist such a UTM that would qualify as a simulating halt decider. However, your intuition is faulty. I know it's easy to identify some patterns that, if they arise during execution, allow us to determine whether the input will halt. However, those patterns will never be comprehensive. No matter how many patterns you write down, there will always be some inputs that aren't handled by any of those patterns.

Those of us who have studied complexity theory already know this, because there is a theorem that proves it. High-level statements such as "Certain patterns of behavior such as infinite loops and infinite recursion can be recognized." is not likely to be effective at persuading anyone to the contrary, because we know there are also other kinds of behavior that won't be recognized; yet such language is too vague and imprecise to allow us to give you specific examples to help you see that fact concretely.

---

If you'd like to pump your intuition, you can find some examples of programs where no one knows whether they halt or not: What are the simplest examples of programs that we do not know whether they terminate?, What are very short programs with unknown halting status?. If you study them, perhaps it will give you a better sense why these programs might fail to halt (they might run forever) without ever entering any loop, or even matching "pattern" that you can write down. (More specifically, for any pattern or list of patterns you have in mind, there might be some input that fails to halt but doesn't match any of those patterns.)

---

If you want an analogy, I find your assertions to come off (to me) as similar to the following made-up conversation:

Polly: Let's define an "awesome circle" to be a circle whose radius $r$ and circumference $C$ satisfy the relationship $C=8r+1$. What would happen if we replaced the 4 tires on my car with objects that have an "awesome circle" shape?

Conan: You can't. No such object exists. The question is meaningless.

Polly: Sure, but assume $H$ is an awesome circle, and I put it on my car. What happens?

Conan: You can't. $H$ doesn't exist. The assumption is false.

Polly: But my $H$ is defined to be awesome. An awesome circle is one that has been adapted so that $C=8r+1$.

Conan: You can't. You can't adapt a circle that way.

Polly: I have superior knowledge of round shapes. Anyone with my experience with round shapes would see immediately how to adapt a circle in that way.

I hope you can see how this exchange is a bit absurd and Conan would tire of it quickly and not have any interest in continuing the conversation. Of course, if Conan knows some mathematics, then he immediately knows that all circles satisfy the relationship $C=2\pi r$; since there is no solution to the system of equations $C=2 \pi r$, $C=8r+1$ with $r \ge 0$, any mathematician would immediately know that no "awesome circle" can exist, so there is not much point in continuing such a conversation.

This is how your attempts to address this topic come off to me. Your assertions remind me of Polly's assertions (Polly's awesome circle = your simulating halt decider; Conan = any computer scientist who has studied decidability). Hopefully this helps you better understand the reactions you are getting and use it to help you focus your future studies.

Answer 2

In response to an earlier version:

You have misunderstood their proof, which is not very well presented (imho); but you also seem to have cut off the end, where they establish the contradiction.

They do not state anywhere that $M$ is simulated, at all.

$\hat H$ simulates $H'$ and $H'$ simulates $H$. Now, $H$ is assumed -- towards a contradiction -- to be decider. which means it always terminates after finitely many steps. No assumption is made on how it solves the halting problem -- which is the point, of course, because only so can be disprove all candidates for $H$ by leading the assumption to a contradiction!

So we simulate $H$ which always terminates -- no infinitely nested simulation is happening.

Your intuition is not wrong, though, even though you seem to be missing the corner cases: you'd need something like "infinitely nested simulation" to solve the halting problem -- something that doesn't work. Because it's impossible.

---

When we hypothesize that the halt decider embedded in Ĥ is simply a Universal Turing Machine (UTM) does this define a computation that never halts when Ĥ is applied to its own Turing machine description?

There are infinitely many UTMs. Without further assumptions, we just don't know what any arbitrary one of those does on its own encoding.

Answer 3

When a simulating halt decider correctly simulates N steps of its input it derives the exact same N steps that a pure UTM would derive because it is itself a UTM with extra features.

Because of this we can know that the first N steps of ⟨Ĥ⟩ simulated by embedded_H are the actual behavior that ⟨Ĥ⟩ presents to embedded_H for these same N steps.

computation that halts… “the Turing machine will halt whenever it enters a final state” (Linz:1990:234)

Ĥ.q0 ⟨Ĥ⟩ ⊢* embedded_H ⟨Ĥ⟩ ⟨Ĥ⟩ ⊢* Ĥ.qy ∞
Ĥ.q0 ⟨Ĥ⟩ ⊢* embedded_H ⟨Ĥ⟩ ⟨Ĥ⟩ ⊢* Ĥ.qn

When Ĥ is applied to ⟨Ĥ⟩
(Ĥ.q0) The input ⟨Ĥ⟩ is copied then transitions to embedded_H
embedded_H is applied to ⟨Ĥ⟩ ⟨Ĥ⟩ (input and copy)
which simulates ⟨Ĥ⟩ applied to ⟨Ĥ⟩
which begins at its own simulated ⟨Ĥ.q0⟩ to repeat the process.

When we see (after the above N steps) that ⟨Ĥ⟩ correctly simulated by embedded_H cannot possibly reach its simulated final state of ⟨Ĥ.qn⟩ in any finite number of steps of correct simulation then we have conclusive proof that ⟨Ĥ⟩ presents non-halting behavior to embedded_H.

Therefore when embedded_H aborts the simulation of its input and transitions to its own final state of Ĥ.qn it is merely reporting this verified fact.

Answer 4

Refutation of the Peter Linz Halting Problem proof

The following shows how Linz H ⟨Ĥ⟩ ⟨Ĥ⟩ gets the right answer because Linz Ĥ.H ⟨Ĥ⟩ ⟨Ĥ⟩ gets the wrong answer

H ⟨Ĥ⟩ ⟨Ĥ⟩ ⊢* H.qy // Ĥ applied to ⟨Ĥ⟩ halts
H ⟨Ĥ⟩ ⟨Ĥ⟩ ⊢* H.qn // Ĥ applied to ⟨Ĥ⟩ does not halt

Criterion Measure
H is assumed to be a simulating termination analyzer that aborts the simulation of any input that would cause its own non-termination and returns NO. Otherwise H always returns YES.

Ĥ.q0 ⟨Ĥ⟩ ⊢* Ĥ.Hq0 ⟨Ĥ⟩ ⟨Ĥ⟩ ⊢* Ĥ.Hqy ∞ // Ĥ applied to ⟨Ĥ⟩ halts
Ĥ.q0 ⟨Ĥ⟩ ⊢* Ĥ.Hq0 ⟨Ĥ⟩ ⟨Ĥ⟩ ⊢* Ĥ.Hqn // Ĥ applied to ⟨Ĥ⟩ does not halt

Execution trace of Ĥ applied to ⟨Ĥ⟩
(a) Ĥ.q0 The input ⟨Ĥ⟩ is copied then transitions to Ĥ.H
(b) Ĥ.H applied ⟨Ĥ⟩ ⟨Ĥ⟩ (input and copy) simulates ⟨Ĥ⟩ applied to ⟨Ĥ⟩
(c) which begins at its own simulated ⟨Ĥ.q0⟩ to repeat the process
Same execution trace even when infinite loop is removed

It is true that Ĥ.H ⟨Ĥ⟩ ⟨Ĥ⟩ must transition to Ĥ.Hqn to prevent its own infinite execution. It is true that this makes Ĥ ⟨Ĥ⟩ halt. This entails that H ⟨Ĥ⟩ ⟨Ĥ⟩ would be correct to transition to H.qy.

When Ĥ.H ⟨Ĥ⟩ ⟨Ĥ⟩ and H ⟨Ĥ⟩ ⟨Ĥ⟩ correctly apply the above criteria then Ĥ.H ⟨Ĥ⟩ ⟨Ĥ⟩ would transition to Ĥ.Hqn and H ⟨Ĥ⟩ ⟨Ĥ⟩ would transition to H.qy

No one has refuted any of the above reasoning