Determining the intersections of a line segment and grid

Question

Problem: Given a line segment on the cartesian plane, determine where and which order it intersects a regular grid. This sounds simple, but is actually quite a tough problem. It's related to, but distinct from, both Bresenham and supercover.

More specifically, consider:

1. A line segment with start $(x_1, y_1)$ and end $(x_2, y_2)$
2. A grid of cells, bounded by all lines $x = k$ and $y = k$ for all integer $k$
3. Each cell therefore has four boundaries, called North, South, East, and West

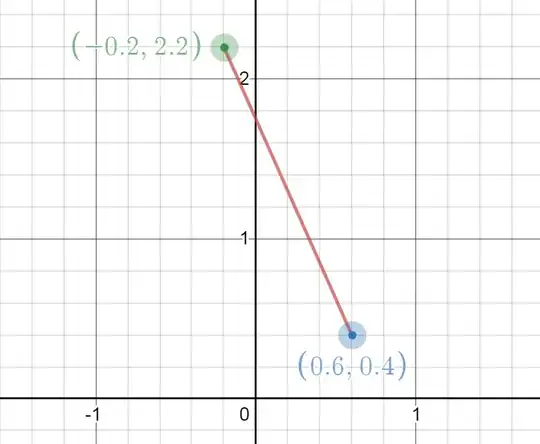
The example plot shows the segment from (0.6,0.4) to (-0.2, 2.2) crossing three boundaries.

For a given line segment, we wish to determine the cell boundaries it crosses:

1. For each boundary type, the number of crossing. {N:2 S:0 E:0 W:1} in the example.
2. The sequence of crossings. {N, W, N} in the example.
3. The grid position of each crossing, defined as $(x - floor(x), y - floor(y))$. Approximately N: (0.35, 1), W: (0, 0.8), N: (0.8, 0) in the example.

I'll note that the problem as-is is not fully defined: line segments starting or ending on a boundary, coinciding with a boundary, and crossing a vertex all need definition. We can accept any reasonable, consistent definition of these.

Solving #1 is easy:

number of east (west if neg) crossings = floor(x2) - floor(x1)
number of north (south if neg) crossings = floor (y2) - floor(y2)

Solving #2 and #3 is surprisingly hard. I've come up with three approaches:

1. Direct. The ideal would be to calculate this directly (that is, without iteration), similar to the formula for #1. I have made no progress here.
2. Iterative. Determine the next crossing (by trying both directions and determining which is crossed first). Determine how far along the segment that is. Repeat until done. This works, though it lacks elegance or speed. The other issue is that chopping the segment repeatedly, if not done carefully, can cause inconsistency with floating point calculations leading to missed or double crossings.
3. Mixed. Use the calculation above to determine the total number of crossings of each type. For each, one $(x,y)$ coordinate is an obvious integer, and the other can be solved using simple algebra, as can the length of the segment to that point. Sort by segment length.

#3 is the best approach so far. Is it possible to do better?

Answer 1

I suggest using a simple iterative method.

Let's first find the places where it crosses a vertical grid lines. These are places where the line goes through a point $(x,y)$ where $x$ is an integer. The points $(x,y)$ on the line can be written in the form

$$(x,y) = (x_0,y_0) + t (x_1-x_0,y_1-y_0),$$

where $(x_0,y_0),(x_1,y_1)$ are the two endpoints of the line and $t \in [0,1]$ is a free variable. Now this point crosses a vertical grid line if $x$ is an integer, i.e., if $x_0 + t(x_1-x_0)$ is an integer. This has solutions of the form $t = (i - x_0)/(x_1-x_0)$, where $i$ is an integer with $x_0 \le i \le x_1$.

Therefore, to find all places where the line crosses a vertical grid line, you can iterative over $i$ in the range $\lceil x_0 \rceil,\dots,\lfloor x_1 \rfloor$, and for each such $i$, compute $t = (i - x_0)/(x_1-x_0)$ and then compute the point $(x,y) = (x_0,y_0) + t (x_1-x_0,y_1-y_0)$. This enumerates all such points on the line.

You can repeat the same for places where the line crosses a horizontal grid line, i.e., where $y$ is an integer. You can then merge these two sequences, sorting them by increasing value of $t$ (note that no sort operation is needed as the list of horizontal crossings and the list of vertical crossings are both already sorted; you just need to merge these two sorted lists).

The running time is linear in the number of such points. This is asymptotically optimal; obviously any algorithm to output all such points must take at least $O(1)$ time per point, so needs to take at least linear time.

This does not have problems with accumulation of floating point errors, as far as I can see. I don't see how this would cause missed or double crossings. I find it elegant, though of course that is a matter of personal taste.