As Yuval pointed out, there is some ambiguity of the original exercise as the enqueueing order of the neighbors of a node is not stipulated by the definition of a breadth-first-search (BFS).
Proposition 1: Let $G$ be a simple undirected connected graph and $e$ is one of its edges. If $e$ is a part of a cycle, then there is a BFS of $G$ that produces a BFS tree that does not contain $e$. (If $e$ is not part of any cycle, then it is a bridge of $G$ and, hence, appears on every spanning tree.)
Since this proposition is, apparently, clear to the OP, no formal proof will be given here.
If we stick to this (indeterministic) version of BFS, the answer to the exercise should be choice 1, "it does not belong to any cycle".
Let us add some context so that that exercise becomes more interesting.
Suppose that for every node, the order of its children to be enqueued in a BFS is fixed beforehand. Now, it can happen that an edge that is part of a cycle can be part of the spanning tree produced from each of $n$ BFS runs. For example, graph $G_1$ with $C_0=[1,3]$, $C_1=[0,2]$, $C_2=[1,3]$, $C_3=[2,0]$, where $C_i$ is the list of neighbors of node $i$ in the enqueueing order. The following lists shows the edge $\overline{1,2}$ is always part of the BFS tree produced.
- The BFS starting from node 0 produces the tree with edges $\overline{0, 1}$, $\overline{0,3}$, $\overline{1,2}$.
- The BFS starting from node 1 produces the tree with edges $\overline{1, 0}$, $\overline{1,2}$, $\overline{0,3}$.
- The BFS starting from node 2 produces the tree with edges $\overline{2, 1}$, $\overline{2,3}$, $\overline{1,0}$.
- The BFS starting from node 3 produces the tree with edges $\overline{3, 2}$, $\overline{3,0}$, $\overline{2,1}$.
We have the following proposition.
Proposition 2: Let $G$ be a simple undirected connected graph and $e$ is one of its edges. Suppose we have selected an enqueueing order for the neighbors of each node. If a BFS of $G$ will always include $e$, then $e$ is either not part of any cycle or $e$ is a part of cycle of even length.
Proof. For the sake of contradiction, suppose that there is a cycle of odd length that contains $e$ and every cycle that contains $e$ is of odd length.
Consider $\mathcal C$, one of the shortest cycles that contains $e$. Since the length of $\mathcal C$ is odd, we can select $v_0$, a node of $\mathcal C$ that is "opposite" to $e$, i.e, the cycle is $v_0, v_1, \cdots, v_k, v_{k+1},\cdots, v_{2k-1}, v_{2k}, v_0$ for some $k$ and $v_i$'s, where $\overline{v_k,v_{k+1}}$ is edge $e$. Since any cycle containing $e$ must be longer than $\mathcal C$, we have,
$$\text{distance}(v_0, v_{k}) = \text{distance}(v_0, v_{k+1}) = k.$$
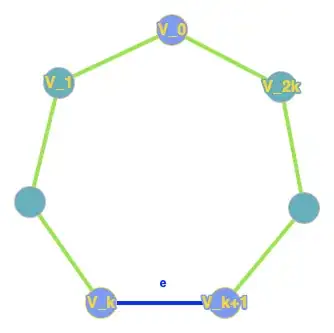
Let us run BFS from node $v_0$. Let tree $T$ be the BFS tree produced. We claim $T$ does not contain $e$. Otherwise, suppose $T$ does contain $e$. WLOG, suppose $v_k$ is nearer to $v_0$ than $v_{k+1}$. Since $T$ is a shortest-path tree from $v_0$, we have
$$\text{distance}(v_0, v_{k+1}) = \text{distance}(v_0, v_{k}) + \text{distance}(v_k, v_{k+1})=\text{distance}(v_0, v_{k}) + 1,$$
which contradicts previous equality. This contradiction shows that $T$ does not contain $e$. That, however, contradicts the given condition that every BFS tree contains $e$. $\ \checkmark$
With respect to proposition 2, the answer to the exercise should be choice 3, "$e$ might belong to a cycle but if it belongs to an odd-length cycle, then it must belong to an even-length cycle.", if the context, i.e. the way in which BFS is supposed to run, implies that the enqueueing order of neighbors of a node is fixed before all runs.
