Understanding connection between length of codeword and hamming distance in Hamming code

Question

I came across following in Huffman coding:

Minimum Hamming distance to correct up to s errors is $2s + 1$ because that way the legal codewords are so far apart that even with $s$ changes the original codeword is still closer than any other codeword.

Then I came across following:

Consider dataword length of $m$ bits, codeword length of $n$ bits. So redundant check bits will be $n-m = r$. Each of the $2^m$ legal messages has $n$ illegal codewords at a distance of $1$ from it. These are formed by systematically inverting each of the $n$ bits in the $n$-bit codeword formed from it. Thus, each of the $2^m$ legal messages requires $n+1$ bit patterns dedicated to it. Since the total number of bit patterns is $2^n$, we must have $(n+1) 2^m ≤ 2^n$.

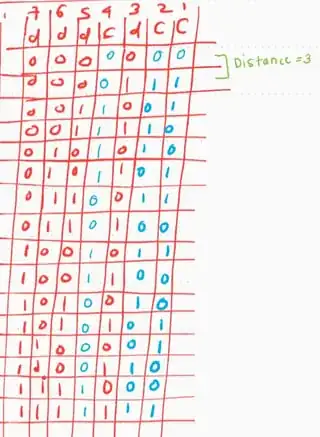
Using this information, I took $m=4$ and found that to meet above equation, $n \ge 7$. So with $n = 7$, I prepared Huffman code for $m = 4$ as shown in the image ($d$ are data bits, $c$ are check bits):

The code has hamming distance of 3 which confirms with $2(1)+1 = 3$ as required to correct 1 bit errors.

Q1. But then, how satisfying $(n+1) 2^m ≤ 2^n$ also ensures hamming distance is 3?

Q2. Also what will be equation if I want to correct $k$ bit errors? Will it be $(\binom{n}{k}+1)2^m\leq 2^n$?

Answer 1

The answer to both questions is the sphere-packing bound.

Consider a binary code on $n$ bits with minimum distance $2d+1$ and $M$ codewords. Imagine surrounding each point of the code with a ball of radius $d$, consisting of all points at distance at most $d$ from the point. These balls must be disjoint: if the balls corresponding to $x,y$ contain some point $z$ in common (note that $z$ need not be in the code), then $d(x,y) \leq d(x,z) + d(y,z) \leq 2d$, contradicting the stated minimum distance. Each ball contains $\binom{n}{\leq d} := \sum_{r=0}^{d} \binom{n}{r}$ points, and so $$ M \times \binom{n}{\leq d} \leq 2^n. $$ This is because there are $M$ disjoint balls, each containing $\binom{n}{\leq d}$ points, while in total there are $2^n$ binary strings of length $n$.