NFA to recognize bit strings containing 01111110

Question

Basically, I currently have two ideas but unsure on which is correct for the following question: "The High level data link control protocol (HDLC), is a popular protocol used for point-to-point data communication. In HDLC, data are organised into frames which begin and end with the sequence 01111110. This sequence never occurs within the main body of the frame, only at the beginning and end (in order to avoid confusion).

a.)Design an NFA which recognises the language of binary strings which contain one or more HDLC frames"

My possible solutions:

The next part is to convert to DFA, but I first need to get this part right.

Answer 1

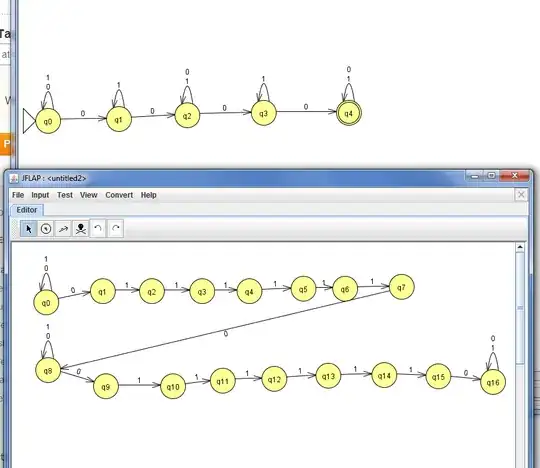
Might as well go for a DFA directly.

First, recognize the string 01111110. If you see something you don't expect, then the information is malformed and you should enter a dead state.

Once you've seen 01111110, start looking for 01111110 again, but this time, if you see something you don't expect, begin looking for 01111110 again from scratch. Once you see a complete 01111110, you have consumed an entire frame, and you should be in an accepting state.

Then, from this halting state, we add the same transitions we have on our initial state; i.e., we leave open the possibility that there are additional frames. Here's a transition table corresponding roughly to what I've indicated:

  State     Input     New State
  q0        0         q1
  q0        1         dead
  q1        0         dead
  q1        1         q2
  q2        0         dead
  q2        1         q3
  q3        0         dead
  q3        1         q4
  q4        0         dead
  q4        1         q5
  q5        0         dead
  q5        1         q6
  q6        0         dead
  q6        1         q7
  q7        0         q8
  q7        1         dead
  // we've seen the leading 01111110
  q8        0         q9
  q8        1         q8
  q9        0         q9
  q9        1         q10
  q10       0         q9
  q10       1         q11
  q11       0         q9
  q11       1         q12
  q12       0         q9
  q12       1         q13
  q13       0         q9
  q13       1         q14
  q14       0         q9
  q14       1         q15
  q15       0         q16
  q15       1         q8
  // we have now seen the trailing 01111110, a whole frame
  // q16 is the only accepting state.
  q16       0         q2
  q16       1         dead

Naturally, you'll want to check that very carefully. If the goal is outputting the message in between the leading and trailing patterns, you might need some extra states to remember input symbols that may or may not be part of the trailing pattern; but for accepting input which consists of a finite number of valid frames, this (or something close to it, if I've made a silly blunder) should be enough.

Answer 2

"Containing 01111110" is easily handled directly with an DFA. Start with something that just recognizes that string; check for each state what you should do to loop back if mismatch (i.e., after 1 if a premature 0 shows up, you have to start over looking for a 1; if the second 0 isn't there, start over at the beginning). After you got your target, anything goes.

Answer 3

The previous answers seem to be incorrect. Let $A = \{0,1\}$. Since you don't want to have the pattern $0110$ as a strict internal factor, the language you are looking can be written as $01111110 A^* 01111110 \setminus 0A^* 01111110 A^*0$. You may use the question Designing a regular expression for the set of all binary that contain strings without a particular sub string (i.e. 110) but you will still have to work a little bit to find the minimal DFA of this language, which has 24 states. The unique final state is 24.

   1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
0  2  0  0  0  0  0  0  9 17 17 17 17 17 17  0 17 17 17 17 17 17 17 24  0  
1  0  3  4  5  6  7  8  0 10 11 12 13 14 15 16 16 18 19 20 21 22 23 16  0

Answer 4

Express the language as a regular expression. Then there is a completely rote method to convert the regular expression to an NFA. I found a particularly good explanation at http://www.csee.umbc.edu/~squire/cs451_l6.html:

While you can represent r⁺ as rr^*, you can actually add a seventh rule that is just like the r^* rule, but leaves out that bottom $\epsilon$ transition:

You can clean up the final NFA at the end by removing any state that has only a single output transition that is also an $\epsilon$ transition. You remove the source state of the $\epsilon$ transition, and merge all of the inputs of the source state into the destination state of the $\epsilon$ transition. This often applies to parts of the NFA created by the concatenation rule (rule 5) and the union rule (rule 4).

I think you will get something similar to your second picture, except note that your original problem called for an NFA that recognizes one or more frames.

Answer 5

I think the regular expression [01]*01111110[01]*01111110[01]* will do. It is not identifying the individual frames, but that wasn't asked either. So this expression is making sure that the string of bits starts with the proper marker and ends with it. Anything can go in between. You can use the method of Wandering Logic to make an NFA out of it. The DFA will be a bit more complicated, but 20 minutes should suffice.