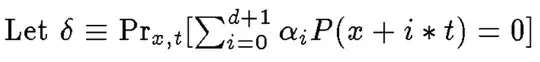Question on the paper ``Self-Testing/Correcting for Polynomials and for Approximate Functions''

Question

I am having some trouble really getting to a precise understanding of some of Self-Testing/Correcting for Polynomials and for Approximate Functions and would greatly appreciate help. Here is my understanding of section 3, Self-Testing Polynomials.

My main problem is that the definition of the function $g$ seems to require a theorem that isn't cited. Details below.

One is given a program $P$. This program (supposedly) computes a polynomial function $f$. This polynomial $f$ is defined implicitly by saying that $f$ is the interpolating polynomial, over some finite field $F$, of data points $(x_0,y_0)$, $(x_1,y_1)$, $\dots$, $(x_n,y_d)$. In other words, $f$ is the lowest degree polynomial satisfying for all $i=0,1,\dots,d$, $f(x_i)=y_i$. In any case, $P$ ought to be very quick to compute, the best case scenario certainly being where $P$ is a list of (supposedly) all values of $f$ pre-computed.

One wants a quick way to verify that $P$ does its job as advertized, at least mostly.

During the proof that the program Polynomial Self-Test has the desired properties, one introduces the function $g$ defined as $$\forall x\in F,\quad g(x)=\mathrm{maj}_{t\in F} \left\{\sum_{i=1}^{d+1}\alpha_i P(x+i\cdot t)\right\}$$ where the $\alpha_i$ are the field elements that satisfy, for any polynomial $Q$ of degree $\leq d$, $$Q(X)=\sum_{i=1}^{d+1}\alpha_i Q(X+i\cdot T)$$ These exist and can be defined in terms of the inverse of a Vandermonde matrix, and the paper even tells us they are binomial coefficients up to a sign.

The goal is nicely summed up by the authors: prove that under certain circumstances, the function $g$ thus ``defined'' is indeed the interpolating polynomial of the data, and mostly agrees with $P$:

It is not clear to me how to interpret the definition of $g$. There are two definitions one could come up with:
1) $g(x)$ is the value that comes up most often from all the $\sum_{i=1}^{d+1}\alpha_i P(x+i\cdot t)$, but this would require us to break ties (probably arbitrarily). This is unacceptable considering a lemma further down that tells us that under certain conditions $g$ is precisely the function $f$ sought after
2) If we consider the totality of values $\sum_{i=1}^{d+1}\alpha_i P(x+i\cdot t)$, for all $t\in F$, there always is a $50\%+\epsilon$ majority of one value. In which case the definition is unambiguous, but which would require a proof, likely saying that if $\delta$ is small enough (and hopefully ``small enough'' can entirely de defined in terms of $d$ and $\delta$, i.e. not using the cardinality $|F|$ of the finite field $F$)

2') Or we could leave $g$ undefined in those cases where no $50\%+\epsilon$ majority arises, but that would surely make the analysis more complicated. 
It seems only the second one makes sense, and when considering a proof that comes afterwards, it seems this is indeed the definition they are using. However, it would require proof that with $\delta$ small enough, a $50\%+\epsilon$ always happens.

Here $1-\delta$ is defined as (I believe there is a typo in the paper here):

When doing a similar analysis with $F_2$-linear maps $F\to F_2$ for a field of characteristic $2$, there is a very cute result from representation theory that tells us that if $f$ satisfies the defining equation of a linear map ``$f(x+y)=f(x)+f(y)$'' often enough, then it agrees with an actual linear map at least as often (in terms of Hamming distance). It seems the authors are aiming for a similar result here, but there is a piece missing as far as I can tell.

Yuval Filmus · Accepted Answer · 2019-06-13T14:27:14.400

The definition of $g$ should be interpreted in the following way:

Any function $g$ for which $g(x)$ is a majority value of $\sum_{i=1}^{d+1} \alpha_i P(x+i\cdot t)$ satisfies what follows.

Since it is later proved that $g = f$, it follows that $g(x)$ is always a strict majority (if it weren't, you would be able to define two different realizations of $g$, and prove that both of them are equal to $f$, contradicting their being different).

If you don't like this interpretation, you could fix a tie-breaking rule and use it to define $g$ conclusively. For example, you could take $g(x)$ to be the smallest majority value of $\sum_{i=1}^{d+1} \alpha_i P(x+i\cdot t)$. The exact tie-breaking rule makes no difference, since the proof shows that it is never actually used.

This kind of definition is common in the literature, and it is best to get used to it. Sometimes the authors explicitly mention that ties can be broken arbitrarily, but otherwise it is just implicitly assumed.

Question on the paper ``Self-Testing/Correcting for Polynomials and for Approximate Functions''

1 Answers1