I'm trying to provide a Hennessy-Milner logic formula for CCS expressions that are not (strongly) bisimilar. An example with a sketch:
For each of the following CCS expressions, decide whether they are strongly bisimilar and if no, find a distinguishing formula in Hennessy-Milner logic.
$b.a.Nil+b.Nil$ and $b(a.Nil+b.Nil)$
I first draw these two to get a better understanding as follows (excuse my awful drawing skills but I couldn't figure out how to put it in LaTeX so I used draw.io):
You can clearly see the Right Hand Side could do $b.b$ but the Left Hand Side can't respond to that. And my distinguishing HML formula is $[b]<b>tt$. On the LHS you get: $[b]\{b.a.Nil+b.Nil\} = \emptyset$ and on the RHS you get: $[b]\{b(a.Nil+b.Nil), a.Nil+b.Nil\} = b(a.Nil+b.Nil)$. Therefore this is a valid distinguishing formula.
Hopefully, I made what the exercise is about clear. Now, the following CCS expressions that I have to distinguish are:
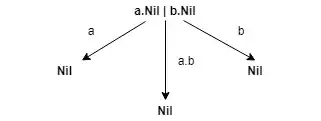
$a.Nil|b.Nil$ and $a.b.Nil + b.a.Nil$.
I know how to draw the RHS because the + denotes a choice but I don't have any idea of how the parallelism work in CCS and couldn't understand it after reading. My guess is the following but it doesn't make sense and is probably wrong:
Could someone help me understand how to sketch the LHS so that I can complete this exercise?
P.S My tags are probably not correct but I couldn't find any tags to Hennessy-Milner logic, so feel free to edit them.