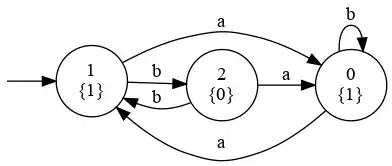
I am dealing with deterministic parity automata and state space reduction (not minimization).
If we define $\equiv_L$ to be the equivalence relation that sets two states equal iff starting from those states the automaton recognizes the same $\omega$-language, merging those states is in general not an operation that preserves language. The canonical example is a parity automaton with two states $q_a, q_b$ that moves to $q_a$ whenever reading an $a$ and to $q_b$ whenever reading a $b$. Giving both states a different parity yields a counter example.
Now what if we refine this relation so that $p \sim q$ is true iff $p \equiv_L q$ and in addition the two states have to have the same color assigned to them. I feel like there has to be a counter example but I can't think of one. That is my question; what is a simple counter example that shows that merging states like this can alter the langauge?
(in case it is not clear what I mean by "merging": merging $p$ and $q$ means removing $q$ from the automaton and redirecting all transitions that would move into $q$ to target $p$ instead)