Behaviour of Dijkstra in Case of Negative Edge Weight

Question

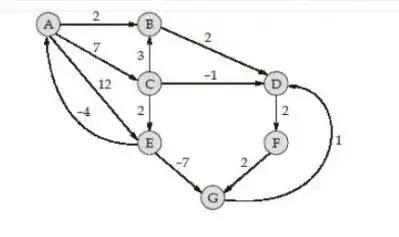
I came across a serious doubt regarding the implementation of the Dijkstra algorithm and hence wanted to discuss.

For the given below graph

What should be the Cost to reach Node G from Source Vertex A?

I was getting 2, as vertex E is the last processed vertex and when it was being processed

$E.d=9,(E,G)=-7$ so $G.d=2$ changed.

Some implementation of Dijkstra says that once a vertex v has been relaxed, then it's estimated $v.d$ is never changed.

Like here

https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/

Here $v.d$ is changed only when sptSet[v] for that vertex is false, means that vertex was not processed before.

But CLRS says that for each vertex U that belongs to queue and results from U=EXTRACT_MIN(Q), we relax all edges leaving U.

So, If I follow the implementation of Dijsktra of what is given in CLRS, I get cost of 2 to reach node G from source Vertex A.

Please guide what should be correct.I am really confused about it.

Answer 1

The article on Dijkstra's algorithm at GeekForGeeks say "Dijkstra’s algorithm doesn’t work for graphs with negative weight edges in general."

Introduction to Algorithms by Corman et al. says "Dijkstra’s algorithm solves the single-source shortest-paths problem on a weighted, directed graph for the case in which all edge weights are nonnegative."

As explained in the linked question and answer and as OP has found, the general proof of the correctness of Dijkstra's algorithm will fail if there are negative edges, hence discussing Dijkstra on graphs with negative weight edges doesn't make sense.

I would advise you to stay away from Dijkstra’s algorithm when a graph that has negative weights appears. It might work in some cases, but it may lead you into troubles that will be avoided if you apply Bellman–Ford algorithm or Floyd–Warshall algorithm.

By the way, the shortest distance from $A$ to $G$ is 2.