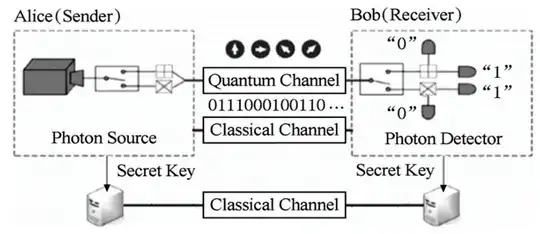
I am currently implementing some QKD protocols using Qiskit and I came up with the following question: After the protocol is finished, a true random password is generated using 0s and 1s, however, and here my question, do these passwords need to be converted to another base? Maybe hexadecimal? Or are they used as they are?
When I mean by used is to using them, for instance, as a key for the one time pad.
As you know, most computers talk in binary " (with only 1s and 0s)". So $E_K(P) = C$ in any base as long as encryption function $E$ is a bijection. Therefore $E'_{K}(C) = P$ reveals the original message. As long as $E$ is deterministic and bijective, the numeric base is kinda irrelevant, but computers do love their octets. [This is not the quantum notation down the fibre optic.]
For example, the following is a cardboard base encoding (and probably before XOR/ASCII was invented):-
59 1 62 62 64. Does this help:-
Notice that (whist preferable) a true one time pad is not required. Conventional symmetrical encryption can be used with regularly changed keys that come through the fibre. So that $|K| \ne |P|$. This greatly helped with throughput but QKDNs are getting pretty fast nowadays.
Is there any chance that you're conflating polarization bases with numeric bases?
Do the bits generated
passwordusing QKD protocols need to be converted to another base before being used as a key for the one time pad?
No, if the OTP encrypts symbols that are bits, as does the most usual OTP.
Yes, in all the other cases. One simple method is rejection sampling: if symbols can take $n$ values, we group input QKD bits by blocks of $b=\left\lceil\,\log_2 n\right\rceil$, convert a block to integer $i$ with $0\le i<2^b$ per e.g. big-endian convention, reject the block if $i\ge n$ (note: which won't happen when $n$ is a power of two), and otherwise use $i$. Among several ways, the OTP can proceed by adding $i$ modulo $n$ for encryption, and subtracting $i$ modulo $n$ for decryption.
But that's arguably the easiest part in QKD. For the difficult ones, see this.
At this step, you can use your key to generate a one-time-pad key with a cryptographic pseudo-random-generator. This functionality takes a fixed-length key as input and output as many bits as you need (if you use it recursively):
https://crypto.stanford.edu/pbc/notes/crypto/prng.html
Then you would use this one-time-pad key by xoring it with a plaintext message of same length. Then you can send classically the ciphertext computed.
Another possibility (more general) is also to use symmetric encryption with the secret key computed by the quantum protocol to encrypt the plaintext message :
https://en.wikipedia.org/wiki/Symmetric-key_algorithm
In any case, you have to be sure than the key length is enough big.
